“两人一般心，无钱堪买金；一人一般心，有钱难买针。”
正文
Matrix是一个3*3的矩阵，通过矩阵执行对图像的平移，旋转，缩放，斜切等操作。先看一段代码
1
2
3
4
5
6
7
8
9
public static final int MSCALE_X = 0; //!< use with getValues/setValues
public static final int MSKEW_X = 1; //!< use with getValues/setValues
public static final int MTRANS_X = 2; //!< use with getValues/setValues
public static final int MSKEW_Y = 3; //!< use with getValues/setValues
public static final int MSCALE_Y = 4; //!< use with getValues/setValues
public static final int MTRANS_Y = 5; //!< use with getValues/setValues
public static final int MPERSP_0 = 6; //!< use with getValues/setValues
public static final int MPERSP_1 = 7; //!< use with getValues/setValues
public static final int MPERSP_2 = 8; //!< use with getValues/setValues
在Matrix中表示为
在研究矩阵之前先来了解一下矩阵的原理，在学过线性代数的都知道，矩阵不具有乘法的交换律。一般情况下图像的点由屏幕上的坐标所确定，屏幕上的坐标一般是由（x，y）所确定，因为Matrix是一个3*3矩阵，所以这里又添加了一个坐标z，在立体空间一个点是由（x,y,z）三个坐标来确定的。如果z越大屏幕就会拉远，图片就会越小。
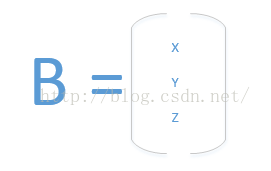
AB相乘结果为
下面就来看一看Matrix的一些主要的方法，
isIdentity
1
2
3
4
5
6
7
/**
* Returns true if the matrix is identity.
* This maybe faster than testing if (getType() == 0)
*/
public boolean isIdentity() {
return native_isIdentity(native_instance);
}
判断矩阵是否是单位矩阵，是就返回true，否则就返回false。所谓单位矩阵就是从左上角到右下角的对角线上的元素均为1。除此以外全都为0的矩阵，也就是下面这种
看一下代码
1
2
3
mMatrix = new Matrix();
mMatrix.setValues(new float[] { 1, 1, 1, 1, 1, 1, 1, 1, 1 });
Log.d("wld_________", mMatrix.isIdentity() + "");
在看一下log
说明上面矩阵不是单位矩阵，再来修改一下代码
1
mMatrix.setValues(new float[] { 1, 0, 0, 0, 1, 0, 0, 0, 1 });
再看一下打印log
打印true，说明上面的矩阵是单位矩阵。
isAffine
isAffine()表示这个矩阵是否是仿射的，仿射变换是从二维坐标到二维坐标之间的线性变换，且保持二维图形的“平直性”和“平行性”，即直线还是直线，曲线还是曲线。仿射变换可以通过一系列的原子变换的复合来实现，包括平移，缩放，旋转，斜切。这类变换可以用一个33的矩阵M来表示，其最后一行为（0，0，1），代入上面AB的公式可以发现原来x，y的坐标并不会对z产生影响，且z方向上的值只会保留不变。该变换矩阵可能会改变线的长度和夹角，但不会改变线段上点的顺序，以及线段之间的比例，比如两个三角形通过仿射变换之后他们的面积比还是不变的，但面积可能会变，更通俗一点讲就是有一束平行的光线通过一个平面把平面上的图像投射到另一个平面上，平面可以是任意角度，但不能与光速平行，这样投影的结果无论是拉伸，平移，旋转还是斜切，都能保证他的整体比例不变，且具有以下性质
1，使共线点变为共线点的双射, 且对应点连线相互平行。
2，平行直线变为平行直线；
3， 保持共线三点的简单比, 从而保持两平行线段的比值不变.
其中最主要一点就是他的平行关系还继续保持，如果平行关系不保持就变成了投影变换。先来看一段代码
1
2
3
mMatrix = new Matrix();
mMatrix.setValues(new float[] { 1, 1, 2, 5, 1, 0, 1, 0, 1 });
Log.d("wld_________", mMatrix.isAffine() + "");
由于最后一行不是0,0,1，所以不是仿射变换矩阵，我们看一下打印log
再来修改一下，让最后一行为0,0,1
1
2
3
mMatrix = new Matrix();
mMatrix.setValues(new float[] { 1, 1, 2, 5, 1, 0, 0, 0, 1 });
Log.d("wld_________", mMatrix.isAffine() + "");
看一下结果，返回true，说明是仿射变换。
具体可以参考：仿射变换矩阵 ，里面介绍的很详细，这里就不在介绍。
rectStaysRect()：判断该矩阵是否可以将一个矩形变换为一个矩形。当矩阵是单位矩阵，或者只进行缩放，平移，以及旋转90度的倍数的时候，返回true。
set(Matrix src)：把src矩阵复制到这个矩阵中，如果src为null，则重置当前矩阵为单位矩阵。
reset()：重置当前矩阵为单位矩阵，我们来看一下
reset
1
2
3
4
5
6
7
8
mMatrix = new Matrix();
mMatrix.setValues(new float[] { 1, 1, 2, 5, 1, 0, 0, 0, 1 });
Log.d("wld_________", mMatrix.isIdentity() + "");
mMatrix.reset();
Log.d("wld_________", mMatrix.isIdentity() + "");
float values []=new float[9];
mMatrix.getValues(values);
Log.d("wld_________", Arrays.toString(values));
再看一下打印log
我们看到刚开始的时候设置的不是单位矩阵，调用reset()方法之后，变成了单位矩阵。
setTranslate
setTranslate(float dx, float dy)，平移操作，因为平移是相对于原来的位置，所以只需要两个参数就够了，我们看一下上面的矩阵A，MTRANS_X和MTRANS_Y是分别表示x方向和y方向的平移量，因为Matrix初始化时候的矩阵是单位矩阵[1,0,0,0,1,0,0,0,1]，假如setTranslate(20, 30)则矩阵变为[1,0,20,0,1,30,0,0,1];假如原来的位置为（x，y，1），代入上面的A*B公式，结果为（x+20,y+30,1），如果用矩阵表示为
其中x0，y0分别为x轴方向和y轴方向的偏移量。我们看一下代码
1
2
3
4
5
6
7
8
mMatrix = new Matrix();
float values[] = new float[9];
mMatrix.getValues(values);
Log.d("wld_________", Arrays.toString(values));
mMatrix.setTranslate(20, 30);
float values1[] = new float[9];
mMatrix.getValues(values1);
Log.d("wld_________", Arrays.toString(values1));
看一下打印结果
我们看到，初始化的时候是单位矩阵，通过平移，矩阵MTRANS_X和MTRANS_Y分别变成了20，和30。通过具体数字可能不是很明白，下面通过一张图来演示一下,先看一下代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class MatrixView extends View {
private Matrix mMatrix;
private Bitmap mBitmap;
private Paint mPaint;
public MatrixView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
mMatrix = new Matrix();
mBitmap = BitmapFactory.decodeResource(getResources(), R.drawable.icon);
mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
mMatrix.setTranslate(100, 200);
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
}
}
看一下运行结果
我们看到图片x轴方向移动100,竖直方向移动200.
setScale
setScale(float sx, float sy, float px, float py)表示图片的缩放，其中sx，sy是缩放的比例，（px，py）是缩放的轴点，关于矩阵的缩放有两个参数MSCALE_X，MSCALE_Y，这个可以自己看一下，就不在介绍，我们看一下代码
1
2
3
4
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
mMatrix.setScale(1.5f, 1.5f, mBitmap.getWidth(), mBitmap.getHeight());
canvas.translate(0, 2*mBitmap.getHeight());
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
上面是原始的图片，然后通过矩阵在x和y方向都放大1.5倍，放大的参照点在图片的右下角位置，为了防止两张图片重叠，我把放大的图片往下移动了一点距离。这个有一点要注意，移动为什么不用之前的setTranslate方法，因为在Matrix中以set开头的方法都会把之前的set清除，这个我们待会再演示，先看一下上面代码的效果图。
我们看到下面的图是比上面的图放到1.5倍，并且以右下角为参照点的。同理，当sx，sy小于1的时候图片会缩小，这个就不在演示，如果为负的会怎么样，我们修改代码看一下
1
2
3
4
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
mMatrix.setScale(-.5f, -.5f, mBitmap.getWidth(), mBitmap.getHeight());
// canvas.translate(0, 2*mBitmap.getHeight());
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
看一下运行结果
再来修改一下代码
1
2
3
4
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
mMatrix.setScale(1, -.5f, mBitmap.getWidth(), mBitmap.getHeight());
// canvas.translate(0, 2*mBitmap.getHeight());
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
看一下结果
x轴方向不变，y轴为负且缩放一半。如果大家看过我之前的Android Paint之ColorFilter详解，是不是可以参照做一个倒影的效果，这个就不在演示。上面说到在matrix的set方法会把之前的矩阵清除，也就是先变为单位矩阵在set，我们结合代码来看一下
1
2
3
4
5
6
7
8
9
10
11
12
13
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
float values1[] = new float[9];
mMatrix.getValues(values1);
Log.d("wld_________", Arrays.toString(values1));
mMatrix.setScale(1, -.5f, mBitmap.getWidth(), mBitmap.getHeight());
float values2[] = new float[9];
mMatrix.getValues(values2);
Log.d("wld_________", Arrays.toString(values2));
mMatrix.setTranslate(100, 100);
float values3[] = new float[9];
mMatrix.getValues(values3);
Log.d("wld_________", Arrays.toString(values3));
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
我们看一下运行结果
我们看到缩放的方法没有执行，只执行了下面的平移方法，因为前面的缩放方法平移的时候重置了，我们看一下打印的log
首先Matrix初始化的时候是单位矩阵，缩放的的时候我们看第二个log，A中的MSCALE_X，MSCALE_Y，MTRANS_Y都变了，其中前两个是缩放的比例，因为缩放的y方向是负的，所以缩放之后的图像往下平移的，所以我们看到MTRANS_Y是有值的，但这个值很奇葩，他是原来图片最上端减去缩放之后图片上端的距离，但缩放之后图片的上端倒过来了，所以他移动的距离相当于图片的高度加上缩放之后图片的高，相当于移动了图片高度的1.5倍，如果我们改一下代码
1
mMatrix.setScale(1,2f, mBitmap.getWidth(), mBitmap.getHeight());
那么会得到MTRANS_Y的值为-462，正好相当于图片的高度，因为图片放大了2倍且没有倒过来，所以相减为负。这里log就不在贴出，我们再看上面的打印的第三个log，把第二个log打印的值清除了，又重新设了值，因为刚才说过Matrix的set方法会清除之前设置的值。如果想要平移，缩放等所有操作都一起设置该怎么办呢，那么就要用到待会下面要讲的pre和post开头的方法了。
setScale(float sx, float sy)和上面的方法类似，表示缩放，不过他的缩放点是在左上角,看一下代码
1
2
3
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
mMatrix.setScale(.3f, .3f);
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
运行结果如下，我们看到参照点是左上角。
为了具体了解图形的缩放，下面来画个图加深一下印象
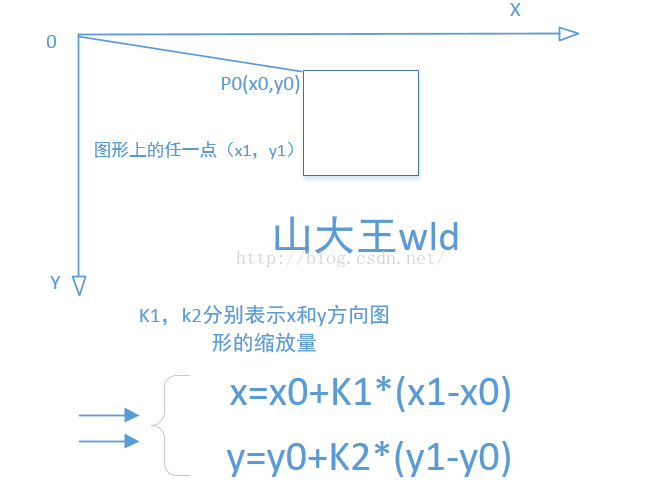
如果用矩阵表示，如下
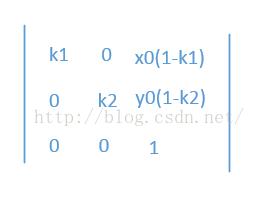
我们来验证一下，看代码
1
2
3
4
5
6
canvas.drawBitmap(mBitmap, 0, 0, mPaint);
mMatrix.setScale(0.4f, .3f, 60, 90);
float values[] = new float[9];
mMatrix.getValues(values);
Log.d("wld_________", Arrays.toString(values));
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
先猜想一下打印的log，其中（60,90）是偏移量，代入上面矩阵得到[0.4,0,36,0,0.3,63,0,0,1],我们再来看一下打印log
结果完全一样。
setRotate
setRotate(float degrees, float px, float py)和setRotate(float degrees)表示旋转，（px，py）表示旋转的参照点，第二个方法的参照点为（0,0），degrees是旋转的角度，当大于360度的时候，会对360求余，看一下代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 原始图
canvas.drawBitmap(mBitmap, 0, 0, mPaint);
// 以（0，0）为参照点旋转60度
mMatrix.setRotate(60);
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
// 以图片右下角为参照点旋转30度
mMatrix.setRotate(30, mBitmap.getWidth(), mBitmap.getHeight());
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
// 画布往下平移
canvas.save();
canvas.translate(0, 2 * mBitmap.getHeight());
// 旋转角度大于360
mMatrix.setRotate(390, mBitmap.getWidth(), mBitmap.getHeight());
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
canvas.restore();
// 画布往下平移
canvas.save();
canvas.translate(0, 2 * mBitmap.getHeight());
// 旋转角度为负
mMatrix.setRotate(-30, mBitmap.getWidth(), mBitmap.getHeight());
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
canvas.restore();
看一下运行结果
我们看到，所有的角度为正的时候全都是按顺时针方向，如果为负的时候是按照逆时针方向旋转的，注意旋转的参考点。我们看到矩阵的数组中有MSCALE（缩放），MSKEW（错切），MTRANS（平移），但我们好像没有看到有旋转的，我们修改一下代码，然后打印一下log
1
2
3
4
5
6
7
8
// 原始图
canvas.drawBitmap(mBitmap, 0, 0, mPaint);
// 以（0，0）为参照点旋转60度
mMatrix.setRotate(60);
float values[] = new float[9];
mMatrix.getValues(values);
Log.d("wld_________", Arrays.toString(values));
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
这个就是上面顺时针旋转60度的图像，就不在贴出，下面我们看一下打印的log
这个大家可能有点迷茫，看不太懂，那么我们就分析一下
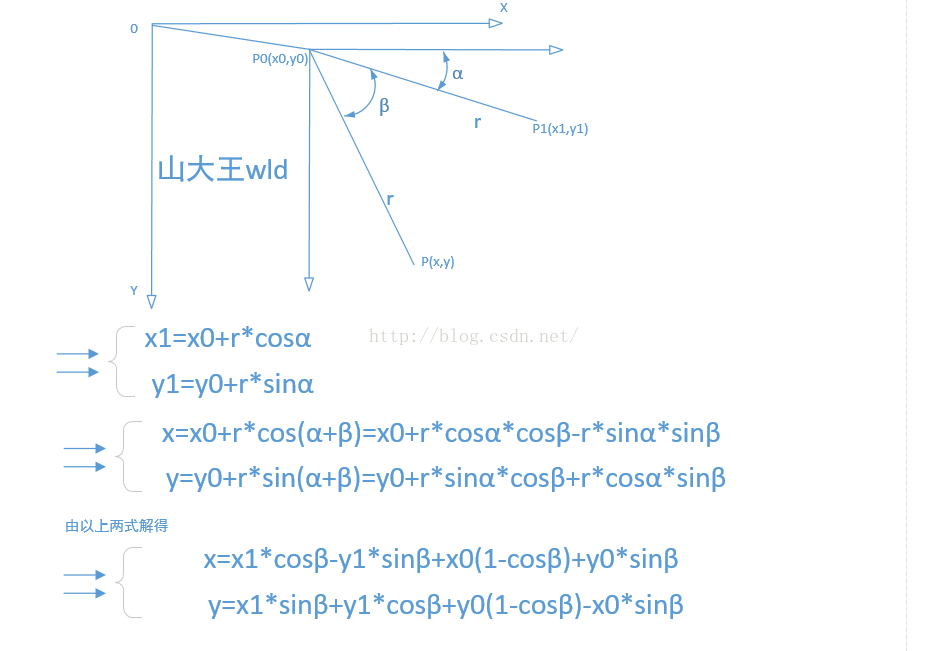
假如有一点为P1，坐标为（x1，y1），绕坐标系中的另一个点p0（x0，y0）旋转，假如p1与水平方向的夹角为α，绕过β角度之后的点为p，坐标为（x，y），则可以通过上面的公式计算出p点的坐标，如果转化为我们这篇所讲的矩阵表示为
通过上面矩阵我们看到，图片的旋转只和旋转的角度β与旋转的参考点（x0，y0）有关，和其他所有的参数一律无关，也难怪setRotate方法中只需要传入旋转的角度和旋转的参考点就可以旋转。上面的矩阵是仿射矩阵，我们还可以把x0，y0提取出来，继续转换
我们看到中间的那个矩阵还可以转化，最终可转化为
OK，分析到这大家应该很明白了吧，先看下面这个矩阵
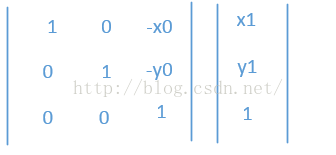
由上面的平移我们知道，当x0，y0为正的时候是往右下角平移的，所以他相当于把p1点往左上角平移了，我们可以这样理解，p1所在的坐标系往右上角平移了（x0，y0），正好p0点和原坐标的原点重合了，然后下面矩阵
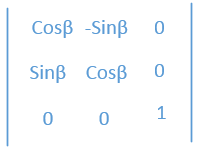
相当于绕原点旋转了β角度，然后看下面的矩阵
相当于又回到了原来的地方，所以这下应该很明白了吧，接着我们来看一下上面打印的log
1
[0.49999997, -0.86602545, 0.0, 0.86602545, 0.49999997, 0.0, 0.0, 0.0, 1.0]
因为上面的图像是围绕原点旋转的，所以x0，y0等于0，β为60度，代入矩阵
所以最终结果为[cos60,-sin60,0,sin60,cos60,0,0,0,1]，正好和上面打印log相差无几，为啥说相差无几，因为cos60是等于0.5，但上面打印的可能由于精度问题导致不等于0.5，不过这并不影响。为了进一步验证，我们在打一下
1
2
3
4
5
6
7
8
// 原始图
canvas.drawBitmap(mBitmap, 0, 0, mPaint);
// 以（0，0）为参照点旋转60度
mMatrix.setRotate(60, 20, 30);
float values[] = new float[9];
mMatrix.getValues(values);
Log.d("wld_________", Arrays.toString(values));
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
这个不是绕原点旋转，我们先不看log，先来分析一下，代入上面矩阵公式，结果应该为[cos60,-sin60,20(1-cos60)+30sin60,sin60,cos60,30(1-cos60)-20sin60,0,0,1],进一步换算[0.5,-sin60,35.98,sin60,cos60,-2.32,0,0,1]，2sin60取的是1.732，我们再来看一下打印的log
结果和我们计算的基本一致。
setSkew
setSkew(float kx, float ky, float px, float py)和setSkew(float kx, float ky)表示错切，很明显后面的方法是相对于原点的操作，我们先来了解一下什么叫做错切，在百度百科上有这样一句话：错切是在某方向上，按照一定的比例对图形的每个点到某条平行于该方向的直线的有向距离做放缩得到的平面图形。在维基百科上是这样描述的
上面所说的错切有两种，一种是水平错切，一种是垂直错切，用我的理解来说是一个矩形拉着他的两个对角，把他变成平行四边形。先画个图来了解一下
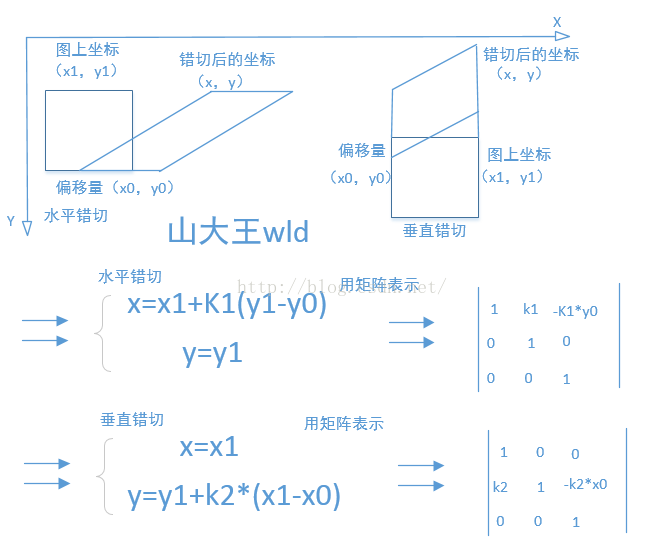
实际上错切应该还有一种就是水平错切和垂直错切结合的，用矩阵表示为
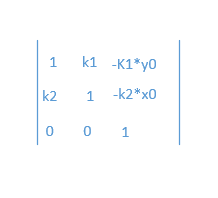
公式推算毕竟太过枯燥，我们还是来看一下实例演示，看代码
1
2
3
4
5
6
canvas.drawBitmap(mBitmap, 0, 0, mPaint);
mMatrix.setSkew(1.5f,1.2f);
float values[] = new float[9];
mMatrix.getValues(values);
Log.d("wld_________", Arrays.toString(values));
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
先不看打印的log，猜想一下log打印的结果，由于相对于原点错切，由上面的矩阵x0,y0都为0，所以最终结果为[1,1.5,0,1.2,1,0,0,0,1];下面来看一下打印的log，验证一下是否正确
我们看到，打印结果和我们猜想的一模一样，再来看一下效果图
他相对于原点错切，也就是相对于左上角，并且x方向和y方向同时错切，在修改一下代码
1
mMatrix.setSkew(0f,.8f);
运行结果
如果修改不同的值，我们会看到意想不到的效果，这里就不在演示。我们再来看一下不是相对原点的错切，看代码
1
2
3
4
5
6
canvas.drawBitmap(mBitmap, 0, 0, mPaint);
mMatrix.setSkew(1.5f, 1.3f, 200, 300);
float values[] = new float[9];
mMatrix.getValues(values);
Log.d("wld_________", Arrays.toString(values));
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
先来猜想一下打印的log，由上面推倒的公式可知结果为[1,1.5,-450,1.3,1,-260,0,0,1],然后看一下打印的log
结果完全一致。顺便再看一下图形
OK，到目前为止，图形的平移，缩放，旋转，错切都已经分析完毕，除了平移以外，其他的都有参考点，当x0，y0都为0的时候是相对于原点的操作，这个是最简单的，可以代入上面的矩阵看一下，这里就不在一一绘出。接着继续来看Matrix的其他方法
setSinCos
setSinCos(float sinValue, float cosValue, float px, float py)，setSinCos(float sinValue, float cosValue)通过指定的sin和cos来设置旋转，我们看到上面旋转的矩阵中包含sin，con以及旋转的参考点，我们一般认为，sin及cos都是小于等于1并且大于等于-1的，但这个方法中我们能不能把sinValue及cosValue的值设置为大于1或小于-1呢，实际上是可以的，这样图形就会放大或缩放或反方向形变，还有一个问题，我们把旋转的矩阵和上面的矩阵A对比一下就会发现，旋转的时候MSCALE_X和MSKEW也跟着变了，也就是说旋转会导致图形缩放和错切，是不是这样的呢，我们先来看一段代码
1
2
3
4
5
Log.d("wld________", "getWidth=" + mBitmap.getWidth() + "&&getHeight=" + mBitmap.getHeight());
canvas.drawBitmap(mBitmap, 0, 0, mPaint);
mMatrix.setSinCos(.866f, .5f,100,100);
Log.d("wld________", "getWidth=" + mBitmap.getWidth() + "&&getHeight=" + mBitmap.getHeight());
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
代码是让图形旋转60度，sin60约等于0.866，cos60为0.5，再来看一下打印的log
在缩放和错切的共同作用下，导致图片的大小并没有改变。
setConcat
setConcat(Matrix a, Matrix b)将矩阵a和b进行合并，我们看一下他的注释
1
2
3
4
5
6
* Set the matrix to the concatenation of the two specified matrices and
* return true.
*
* <p>Either of the two matrices may also be the target matrix, that is
* <code>matrixA.setConcat(matrixA, matrixB);</code> is valid.</p>
*
我们可以这样调用matrixA.setConcat(matrixA, matrixB)，合并的结果是矩阵a与b的乘积除以2，怎么说呢，看一下代码
1
2
3
4
5
6
7
Matrix mMatrix1=new Matrix();
mMatrix1.setValues(new float[]{1,2,3,4,5,6,7,8,9});
Matrix mMatrix2=new Matrix();
mMatrix2.setValues(new float[]{5,1,3,2,2,3,4,5,2});
mMatrix1.setConcat(mMatrix1, mMatrix2);
Log.d("wld_________", mMatrix1.toShortString());
Log.d("wld_________", mMatrix2.toShortString());
很显然，最终的结果会放到mMatrix1中，我们猜一下结果，矩阵mMatrix1与mMatrix2的乘积为[21,20,15,54,44,39,87,68,63]，除以2结果为[10.5,10,7.5,27,22,19.5,43.5,34,31.5]，我们再来看一下打印的log
和计算的结果一模一样。当然如果改为
1
mMatrix2.setConcat(mMatrix1, mMatrix2);
那么计算的结果就会存储到mMatrix2中，如果我们在new一个新的mMatrix3，调用mMatrix3.setConcat(mMatrix1, mMatrix2);，结果就会存储到mMatrix3中。
pre和post
然后接着就是以pre和post开头的一些方法，pre开头的表示前乘，就是矩阵在前面，比如M’ = M * T(dx, dy)，post开头的表示后乘，就是矩阵在后面，比如M’ = T(dx, dy) * M。因为上面说过，以set开头的会把之前的矩阵置为单位矩阵，然后在set，如果想要上面的几种方式一起操作，则需要使用pre或post开头的方法，看代码
1
2
3
mMatrix.setScale(0.4f, .3f);
mMatrix.postTranslate(600, 600);
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
我们暂且可以这样理解，图形先缩放然后在平移，究竟是先缩放还是先平移，这个都不重要，因为他是矩阵相乘的最终结果作用在图形上的，看一下图形所在的位置
下面在修改一下代码
1
2
3
mMatrix.setScale(0.4f, .3f);
mMatrix.preTranslate(600, 600);
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
再看一下图形所在的位置
差别竟那么大，为什么会这样，因为在开头的时候说过矩阵不具有乘法的交换律，矩阵的前乘和后乘可能会出现不同的结果。我们可以想象一下，上面一个图形是先缩放然后在平移（我们暂且这样认为，不管他对不对，因为这样有助于我们理解），那么他的左上角点的坐标肯定为（600,600）。下面一个图形相当于先平移然后在缩放，如果按照我们正常人的思维，我们肯定会认为无论是先平移还是先缩放，最终的位置肯定是一样的，没错，确实只这样。但这里我们忽略了一个问题，就是上面讲的缩放的参考点，上面一个图形的缩放点在图形的左上角，但下面那个图形由于平移，导致他的缩放点不在图形的左上角。如果我们想要和上面一个图形的位置一样，改怎么办呢，我们还可以这样写，看代码
1
2
3
mMatrix.setScale(0.4f, .3f, 600, 600);
mMatrix.preTranslate(600, 600);
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
让他缩放的参考点还是在图形的左上角上就行了，如果想和下面那个图形的位置一样，还可以这样写
1
2
3
mMatrix.setScale(0.4f, .3f,-600,-600);
mMatrix.postTranslate(600, 600);
canvas.drawBitmap(mBitmap, mMatrix, mPaint);
其实这只是一个演示，告诉我们可以这样实现，但在工作中没必要搞这么复杂，知道就行。下面就通过矩阵来了解一下前乘和后乘的区别，先看setScale(0.4f, .3f)，会把单位矩阵置为
然后调用postTranslate(600, 600)，我们知道post是后乘，即M’ = T(dx, dy) * M，之前矩阵在后面，我们看一下相乘的结果
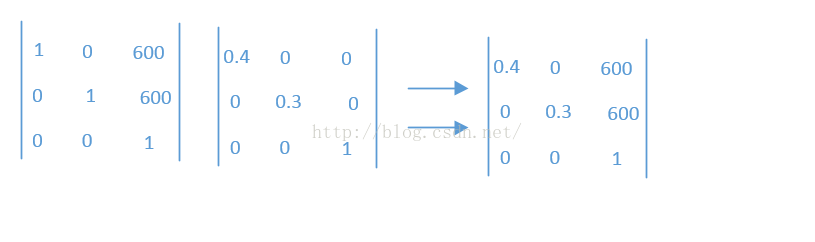我们再来看一下setScale(0.4f, .3f)和preTranslate(600, 600)的结果，pre开头的是前乘，M’ = M * T(dx, dy) ，即之前矩阵在前，我们看一下
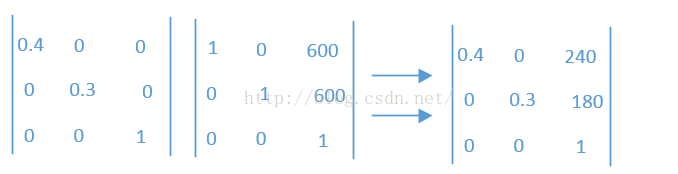
所以两个矩阵交换位置相乘的结果完全不同，上面一个矩阵相当于移动了（600,600），下面一个矩阵相当于移动了（240,180），所以我们看到上面图形中两个位置是不一样的。还有，如果调用了set方法，那么之前的所有set，post和pre开头的方法都将作废，即相当于重置。由于Matrix中平移，缩放，旋转，错切都具有set，pre和post开头的方法，想怎么使用，在工作中可以根据需要来进行自由组合，这里就不在一一演示。
setRectToRect
setRectToRect(RectF src, RectF dst, ScaleToFit stf)，将src矩形的内容填充到dst矩形中，其中ScaleToFit是枚举类，有四种类型，我们看一下注释
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/** Controlls how the src rect should align into the dst rect for
setRectToRect().
*/
public enum ScaleToFit {
/**
* Scale in X and Y independently, so that src matches dst exactly.
* This may change the aspect ratio of the src.
*/
FILL (0),
/**
* Compute a scale that will maintain the original src aspect ratio,
* but will also ensure that src fits entirely inside dst. At least one
* axis (X or Y) will fit exactly. START aligns the result to the
* left and top edges of dst.
*/
START (1),
/**
* Compute a scale that will maintain the original src aspect ratio,
* but will also ensure that src fits entirely inside dst. At least one
* axis (X or Y) will fit exactly. The result is centered inside dst.
*/
CENTER (2),
/**
* Compute a scale that will maintain the original src aspect ratio,
* but will also ensure that src fits entirely inside dst. At least one
* axis (X or Y) will fit exactly. END aligns the result to the
* right and bottom edges of dst.
*/
END (3);
// the native values must match those in SkMatrix.h
ScaleToFit(int nativeInt) {
this.nativeInt = nativeInt;
}
final int nativeInt;
}
首先我们看一下上面的注释，
FILL：表示分别缩放x，y，让src更准确的匹配dst，但这可能会改变src的长宽比。就是不成比例的缩放，完全填充dst
START：表示计算一个合适的值，保留src的长宽比，但要确保src完全在dst中，x，y方向上至少有一个要完全填充dst，要沿着dst的左端和顶端。
CENTER：和上面类似，也是保证缩放的长宽比，也是完全在dst中，也是至少有一个边要完全填充dst，但不同的是他会在dst的中间。
END：和START类似，不过他是沿着dst的右端和底端。
下面老规矩，看代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public class MatrixView extends View {
private Bitmap mBitmapV;
private Bitmap mBitmapH;
private Paint mPaint;
private RectF hSrcRectF;
private RectF hDstRectF;
private RectF vSrcRectF;
private RectF vDstRectF;
private ScaleToFit mScaleToFit[] = { ScaleToFit.CENTER, ScaleToFit.END, ScaleToFit.FILL, ScaleToFit.START };
private Matrix mMatrix;
private TextPaint mTextPaint;
public MatrixView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
mBitmapV = BitmapFactory.decodeResource(getResources(), R.drawable.v);
mBitmapH = BitmapFactory.decodeResource(getResources(), R.drawable.h);
mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
mPaint.setStyle(Style.FILL_AND_STROKE);
mPaint.setColor(Color.BLUE);
hSrcRectF = new RectF(0, 0, mBitmapH.getWidth(), mBitmapH.getHeight());
hDstRectF = new RectF(0, 0, mBitmapH.getWidth() * 1.5f, mBitmapV.getHeight() * 1.5f);
vSrcRectF = new RectF(0, 0, mBitmapV.getWidth(), mBitmapV.getHeight());
vDstRectF = new RectF(0, 0, mBitmapH.getWidth() * 1.5f, mBitmapV.getHeight() * 1.5f);
mMatrix = new Matrix();
mTextPaint = new TextPaint(Paint.ANTI_ALIAS_FLAG);
mTextPaint.setTextSize(56);
mTextPaint.setColor(Color.RED);
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
canvas.drawBitmap(mBitmapH, 260, 100, null);
canvas.drawBitmap(mBitmapV, 700, 100, null);
canvas.drawText("原图", 40, 200, mTextPaint);
for (int i = 0; i < mScaleToFit.length; i++) {
canvas.drawText(mScaleToFit[i].toString(), 40,
100 + (i + 1) * (hDstRectF.height() + 60) + hDstRectF.height() / 2, mTextPaint);
canvas.save();
canvas.translate(300, 100 + (i + 1) * (hDstRectF.height() + 60));
canvas.drawRect(hDstRectF, mPaint);
mMatrix.reset();
mMatrix.setRectToRect(hSrcRectF, hDstRectF, mScaleToFit[i]);
canvas.drawBitmap(mBitmapH, mMatrix, null);
mMatrix.reset();
canvas.translate(400, 0);
canvas.drawRect(vDstRectF, mPaint);
mMatrix.setRectToRect(vSrcRectF, vDstRectF, mScaleToFit[i]);
canvas.drawBitmap(mBitmapV, mMatrix, null);
canvas.restore();
}
}
}
在看一下运行结果
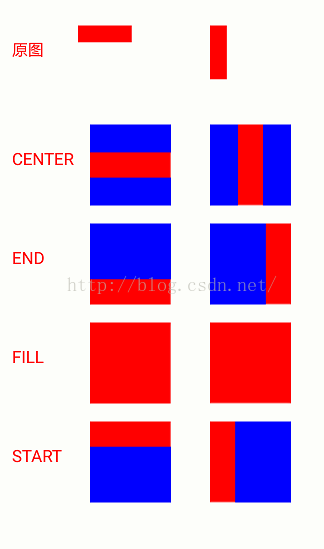
最上面两个是原图，下面的8个图中，蓝色部分是dst，红色是原图进行缩放后的图，比较简单，和上面的描述一模一样，这里就不在分析。这里的dst都是大于src的，如果小于src会怎么样呢，其实他会缩放的，我们修改代码看一下
1
2
3
4
5
hSrcRectF = new RectF(0, 0, mBitmapH.getWidth(), mBitmapH.getHeight());
hDstRectF = new RectF(0, 0, mBitmapH.getWidth() * .5f, mBitmapV.getHeight() * .5f);
vSrcRectF = new RectF(0, 0, mBitmapV.getWidth(), mBitmapV.getHeight());
vDstRectF = new RectF(0, 0, mBitmapH.getWidth() * .5f, mBitmapV.getHeight() * .5f);
看一下运行结果
setPolyToPoly
setPolyToPoly(float[] src, int srcIndex,float[] dst, int dstIndex,int pointCount)表示把图形的四个点映射到另外一个图形中，src是原图的需要映射的坐标，以（x，y）成对出现的，srcIndex指原图映射的起始点，dst指目标图，dstIndex指目标图的起始点，pointCount指映射的点数，最多是4个，左上，右上，左下，右下分别为1，2，3，4四个点，还是先看一段代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
public class MatrixView extends View {
private Matrix mMatrix;
private Path mPath;
private Bitmap mBitmap;
private Paint mPaint;
private Paint mSrcPaint;
private Paint mDstPaint;
public MatrixView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
mMatrix = new Matrix();
mPath = new Path();
mBitmap = BitmapFactory.decodeResource(getResources(), R.drawable.icon);
mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
mPaint.setStyle(Style.STROKE);
mPaint.setStrokeWidth(12);// 防止被下面的线覆盖，画宽一点。
mPaint.setColor(Color.RED);
mSrcPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
mSrcPaint.setStyle(Style.STROKE);
mSrcPaint.setStrokeWidth(8);
mSrcPaint.setColor(Color.BLUE);
mDstPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
mDstPaint.setStyle(Style.STROKE);
mDstPaint.setStrokeWidth(8);
mDstPaint.setColor(Color.YELLOW);
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
canvas.drawBitmap(mBitmap, 0, 0, null);
float src[] = { 0, 0, mBitmap.getWidth(), 0, 0, mBitmap.getHeight(),
mBitmap.getWidth(), mBitmap.getHeight() };
float dst[] = { 300, 300, mBitmap.getWidth() + 100, 30, 100,
mBitmap.getHeight() + 200, mBitmap.getWidth() + 300,
mBitmap.getHeight() + 300 };
float array[] = { 0, 0, mBitmap.getWidth(), 0, 0, mBitmap.getHeight(),
mBitmap.getWidth(), mBitmap.getHeight() };
drawPath(canvas, array, mPaint);
drawPath(canvas, src, mSrcPaint);
drawPath(canvas, dst, mDstPaint);
canvas.translate(0, 800);
mMatrix.setPolyToPoly(src, 0, dst, 0, src.length >> 1);
canvas.drawBitmap(mBitmap, mMatrix, null);
drawPath(canvas, array, mPaint);
drawPath(canvas, src, mSrcPaint);
drawPath(canvas, dst, mDstPaint);
}
private void drawPath(Canvas canvas, float array[], Paint mPaint) {
mPath.reset();
mPath.moveTo(array[0], array[1]);
mPath.lineTo(array[2], array[3]);
mPath.lineTo(array[6], array[7]);
mPath.lineTo(array[4], array[5]);
mPath.close();
canvas.drawPath(mPath, mPaint);
}
}
看一下效果图
他是用原图四个角的坐标映射到另一个四边形中，把蓝色部分映射到黄色部分，为了便于观察，上面一个图形是原始图，下面一个图是映射之后的，当然，我们还可以映射3个点，或2个点，看一下,下面从左往右分别是3个点，2个点，1个点和0个点的映射
3个点和2个点
1个点和0个点
当然，如果只是想映射原图中的一部分，还可以这样改，
1
2
float src[] = { 300, 100, mBitmap.getWidth(), 0, 0, mBitmap.getHeight(), mBitmap.getWidth(),
mBitmap.getHeight() };
看一下运行结果
在修改代码看一下
1
2
float src[] = { 300, 100, mBitmap.getWidth(), 0, 0, mBitmap.getHeight()-100, mBitmap.getWidth()-100,
mBitmap.getHeight() };
看截图
我们可以很明显看到，上面图中把原图截取蓝色部分，然后拉伸放到黄色部分中，下面一个图由于屏幕不够所以左右两边没有完全显示，至于截取之外的部分是怎么排放的，这个就真的不知道了。不过这种方法用的不是很多，一般都是映射原图的四个点，或者映射原图的一部分到一个矩形中，比如网上常见的图片折叠。
invert
public boolean invert(Matrix inverse)如果矩阵可逆，求当前矩阵的逆矩阵并且存入inverse中，如果当前矩阵不可逆，忽略 inverse，返回false， 当前矩阵*inverse（逆矩阵）=单位矩阵，我们看一下代码
1
2
3
4
5
6
7
8
9
10
Matrix mMatrix1 = new Matrix();
Matrix mMatrix2 = new Matrix();
Matrix mMatrix3 = new Matrix();
mMatrix1.setValues(new float[] { 1, 2, 2, 3, 3, 5, 2, 3, 5 });
Log.d("wld________", mMatrix1.invert(mMatrix2) + "");
mMatrix3.setConcat(mMatrix1, mMatrix2);
Log.d("wld________mMatrix1=", mMatrix1.toShortString());
Log.d("wld________mMatrix2=", mMatrix2.toShortString());
Log.d("wld________mMatrix3=", mMatrix3.toShortString());
先不看打印log，分析一下mMatrix1的逆矩阵mMatrix2的值，学过线性代数的都知道逆矩阵的算法，下面来推导一下，可能不是最好的算法，但这都不重要，我们要的只是结果，毕竟过去那么多年，也忘的差不多了，
所以我们看到，最终得到的逆矩阵就是上面的最后3排，也就是【0，1，-1，5/4，-1/4，-1/4，-3/4，-1/4，3/4】，我们再来看一下打印的log
我们看到返回为true，说明上面的矩阵是可逆的，同时还看到打印的mMatrix2正好和我们推导的一样，他就是mMatrix1的逆矩阵，同时还注意到mMatrix3，是一个单位矩阵，他是当前矩阵mMatrix1和他的逆矩阵mMatrix2相乘的结果。但并非所有的矩阵都有逆矩阵，比如下面一个矩阵
1
2
3
4
5
6
mMatrix1.setValues(new float[] { 1, 2, 3, 4, 5, 6, 7, 8, 9 });
Log.d("wld________", mMatrix1.invert(mMatrix2) + "");
mMatrix3.setConcat(mMatrix1, mMatrix2);
Log.d("wld________mMatrix1=", mMatrix1.toShortString());
Log.d("wld________mMatrix2=", mMatrix2.toShortString());
Log.d("wld________mMatrix3=", mMatrix3.toShortString());
看一下打印log
我们看到，返回为false，说明这个矩阵是不可逆的，同时还看到mMatrix2是一个单位矩阵，并不是mMatrix1的逆矩阵。在改一下代码看一下
1
2
3
4
5
6
7
8
mMatrix1.setValues(new float[] { 1, 2, 2, 3, 3, 5, 2, 3, 5 });
// mMatrix1.setValues(new float[] { 1, 2, 3, 4, 5, 6, 7, 8, 9 });
Log.d("wld________", mMatrix1.invert(mMatrix2) + "");
// mMatrix3.setConcat(mMatrix1, mMatrix2);
mMatrix2.invert(mMatrix3);
Log.d("wld________mMatrix1=", mMatrix1.toShortString());
Log.d("wld________mMatrix2=", mMatrix2.toShortString());
Log.d("wld________mMatrix3=", mMatrix3.toShortString());
看一下打印log
我们看到mMatrix1和mMatrix3是一样的，这说明逆矩阵的逆矩阵还是原矩阵。那么逆矩阵有什么作用呢，其实就相当于整数的倒数一样，逆矩阵和原矩阵相乘等于单位矩阵，矩阵中没有直接相除的概念，那么逆矩阵就可以实现矩阵相除。我们看一下代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public class MatrixView extends View {
private Matrix mMatrix1;
private Matrix mMatrix2;
private Bitmap mBitmap;
private Paint mPaint;
public MatrixView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
mBitmap = BitmapFactory.decodeResource(getResources(), R.drawable.icon);
mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
mPaint.setColor(Color.RED);
mPaint.setStyle(Style.FILL_AND_STROKE);
mPaint.setStrokeWidth(8);
mMatrix1 = new Matrix();
mMatrix2 = new Matrix();
mMatrix1.setValues(new float[] { 1, 2, 2, 3, 3, 5, 2, 3, 5 });
mMatrix1.setTranslate(100, 200);
Log.d("wld________", mMatrix1.invert(mMatrix2) + "");
Log.d("wld________mMatrix1=", mMatrix1.toShortString());
Log.d("wld________mMatrix2=", mMatrix2.toShortString());
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
canvas.translate(300, 300);
canvas.drawBitmap(mBitmap, mMatrix1, null);
canvas.drawBitmap(mBitmap, mMatrix2, null);
canvas.drawLine(0, 0, getMeasuredWidth(), 0, mPaint);
}
}
看一下运行结果
为了防止变换之后部分看不到，我把canvas往下移动了红线的距离，我们看到最下面的图是mMatrix1变换得到的，在前面说过矩阵的set方法会先把当前的矩阵置为单位矩阵，所以他只是往下平移了200，往右平移了100，在看上面那张图是由mMatrix2变换得到的，好像和下面那张图正好相反，应该是平移了（-100，-200），我们看一下打印log
看的没，正好和我们猜的一样，这回逆矩阵的一些性质我们应该很清楚了吧，下面在把上面代码修改一下
1
mMatrix1.setRotate(60);
直接上图
打印log
在修改
1
mMatrix1.setScale(.5f, .8f);
图形一个会变大一个会变小，这个会重叠，需要移动一点距离才能看的更加明白，就不上传了，看一下打印log
继续修改
1
mMatrix1.setSkew(.3f, .5f);
看一下运行结果
再看一下log
这回我们知道逆矩阵的原理了吧，和原矩阵是对着干的，至于他是怎么得到的，可以按照上面逆矩阵的推算来得到，这里就不可能一一来推算了。
mapPoints
mapPoints(float[] dst, int dstIndex, float[] src, int srcIndex,int pointCount)，mapPoints有几个重载的，这里就拿这个来分析，他指的是映射点的值到指定的数组中，他可以在矩阵变换以后，给出指定点的值，我们找个简单的看一下
1
2
3
4
5
6
7
mMatrix1 = new Matrix();
mMatrix1.setScale(.3f, .5f);
float src[] = { 20, 20, 100, 100 };
float[] dst = new float[4];
mMatrix1.mapPoints(dst, 0, src, 0, dst.length >> 1);
Log.d("wld________mMatrix1=", mMatrix1.toShortString());
Log.d("dst=", Arrays.toString(dst));
(20,20)和（100,100）是原图形上的点，通过矩阵缩放后，应该为（6,10）（30,50），看一下打印log
结果和预想一样，不过那个30.000002可能是由于精度问题有一点点偏差，不过这并不影响。
mapVectors
mapVectors(float[] dst, int dstIndex, float[] src, int srcIndex,int vectorCount) 他也有几个重构的方法，这里也只分析这一个。他是改变向量然后存储在dst中，我们知道向量是可以移动的，所以他对平移式不起作用的，来看一下他的注释就明白了
1
2
3
4
5
6
7
8
/**
* Apply this matrix to the array of 2D vectors specified by src, and write
* the transformed vectors into the array of vectors specified by dst. The
* two arrays represent their "vectors" as pairs of floats [x, y].
*
* Note: this method does not apply the translation associated with the matrix. Use
* {@link Matrix#mapPoints(float[], int, float[], int, int)} if you want the translation
* to be applied.
可以把上面代码改一下
1
mMatrix1.mapVectors(dst, 0, src, 0, dst.length >> 1);
打印log还是和之前的一样，基本没有变化
mapRect
mapRect(RectF dst, RectF src)测量矩形变换后的位置，如果返回任为矩形返回true，否则返回false，他只会记录变换之后图形的左上角及右下角的坐标，看一下代码
1
2
3
4
5
6
7
8
mMatrix1 = new Matrix();
mMatrix1.setScale(.3f, .5f);
RectF src = new RectF(0, 0, mBitmap.getWidth(), mBitmap.getHeight());
RectF dst = new RectF();
Log.d("mapRect=", mMatrix1.mapRect(dst, src) + "");
Log.d("wld________mMatrix1=", mMatrix1.toShortString());
Log.d("src=", src.toShortString());
Log.d("dst=", dst.toShortString());
看一下打印log
src经过缩放之后等于dst，且返回true，说明缩放之后还是矩形，其实不打印也能猜的出来，矩形的缩放，平移之后还是矩形，在来修改一下，这回不让他缩放了，让他旋转
1
mMatrix1.setRotate(60);
我们看到返回false，说明旋转就不在是矩形了，这个可能不太好理解，我们看到旋转之后之前的两个点的位置变化了，感觉图形是变大了，旋转之后记录的是图形所在外矩形框的左上角和右下角坐标，旋转之后图形大小实际上没变，因为我们前面分析过在旋转的时候矩阵的错切参数也会跟着变化（或者我们看上面的旋转公式也可以看得出来），所以旋转之后外框是变大了，但是在旋转和错切的共同作用下导致图像大小并不会改变，再改一下
1
mMatrix1.setRotate(90);
看一下log
我们看到是返回了true，说明矩形旋转90度之后还是矩形，我们还可以参考最上面讲的rectStaysRect()方法。当图形执行错切的时候会返回false，改一下来看看
1
mMatrix1.setSkew(.3f, .7f);
因为错切之后矩形就不再是矩形了，所以返回false。
mapRadius
mapRadius(float radius)一个圆经过矩阵变换之后的半径，是个平均值，因为有可能是椭圆，看一下代码
1
2
3
mMatrix = new Matrix();
mMatrix.setTranslate(120, 160);
Log.d("dst=", mMatrix.mapRadius(100) + "");
看一下log
我们看到平移的时候半径是不会变的，在修改一下
1
mMatrix.setScale(.5f, .5f);
看一下打印log
其实这个我们猜也能猜得到，因为都缩放一半，所以半径自然会缩放一半，下面在改一下
1
mMatrix.setScale(.5f, 1.5f);
这回变成了长为300，宽为100的椭圆了，那么椭圆的公式变成了x^2/150^2+y^2/50^2=1(^2表示平方的意思)，他的半径不好求，那么我们求他的面积然后按照圆的面积计算公式计算出半径，我们知道椭圆的面积为S=π(圆周率)×a×b（其中a,b分别是椭圆的半长轴，半短轴的长），那么他的面积为π15050=750π，由圆的面积S=π*r^2，所以计算出半径约为86.602540378，我们看一下打印log
和我们计算基本一致。
OK，到目前为止，Matrix基本已经分析完毕。
