“相见易得好,久住难为人。”
正文
对于Integer这个类估计大家也都非常熟悉了,以前看过他的源码,但也只是粗略的看了一下,最近有时间认真的看了一下发现这个类设计的非常好,所以就打算记录下来与大家共享。我们看一下java项目中的Integer类大概有500多行,并且注释也很少,
而Android中的Integer大概有1000多行,当然他的注释也比较多
既然是要分析,那么就索性两个一起来分析,这里我以Android中的Integer为主,是挑着来分析的,不是按顺序的,先看一下bitCount(int i)这个方法
bitCount
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
* Returns the number of one-bits in the two's complement binary
* representation of the specified {@code int} value. This function is
* sometimes referred to as the <i>population count</i>.
*
* @return the number of one-bits in the two's complement binary
* representation of the specified {@code int} value.
* @since 1.5
*/
public static int bitCount(int i) {
// HD, Figure 5-2
i = i - ((i >>> 1) & 0x55555555);
i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
i = (i + (i >>> 4)) & 0x0f0f0f0f;
i = i + (i >>> 8);
i = i + (i >>> 16);
return i & 0x3f;
}
他表示的是计算int类型转化为二进制之后1的个数,举个例子,5用二进制表示为101,那么就返回2,表示有2个1,8用二进制表示是1000,就会返回1,表示有一个1.但是这个方法用的非常妙,直接看可能不是太明白,如果把上面的数字转化成二进制可能就会明白很多,0x55555555用二进制表示就是……01010101(1个0,1个1循环,总共是32位),0x33333333用二进制表示就是……00110011(2个0,2个1循环,总共32位),0x0f0f0f0f用二进制表示就是……0000111100001111(4个0,4个1循环,总共32位),看到这里可能就会稍微有点明白,其实他的原理就是每两位为一个小的单元,计算出1的个数储存在两位数中,然后再以4位为一个小的单元计算前面储存的数的和,储存到4位数中,然后再以8位,16位,以此类推。但这里要注意第一行和后面的几行原理是不同的,第一行是计算1的个数,后面的几行都是对第一行计算的结果相加,举个例子,比如第一行开始计算的时候如果最后两位二进制数为10,那么他表示最后两位只有一个1,因为还一个为0,如果是后面的几行,那么开始计算的时候如果二进制为10,那么他表示最后两位数有2个1,因为从第二行开始每个位上的1和0不在是表示1和0了,他表示的是第一行1和0的个数的和,而二进制10就是十进制2的意思,所以他表示的是2个1。其实第一行很好理解,i往右移动一个单位,再与……01010101(32位)进行与运算,就表示把原来的偶数位变为奇数位,然后再把新的偶数位置为0,再用i减去他,他表示的是把一个数每两个分为一组,然后让每组中的数减去这个组的偶数位上的数字,所以他最终表示的结果就是每两位1的个数储存在原来的两位数中,我画个图就好理解了

我还是写在代码里逐行分析可能会更好一些,下面是代码的分析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public static int bitCount(int i) {
// HD, Figure 5-2
/**
* 每两位为一个单元,把原来单元中1的个数储存在原来的单元中
*/
i = i - ((i >>> 1) & 0x55555555);
/**
*0x33333333其实就是二进制……00110011(共32位),因为上面的每两位代表1的个数,所以下面的这几行就是要把上面每两位
* 的数字加起来,下面的这行代码可以这样理解,每4位分为一组,然后4位中的每两位相加,相加的结果在储存到这4位二进制数中,
* i & 0x33333333表示每4位中的低2位,(i >>> 2) & 0x33333333表示每4位中的高2位,然后在相加
*/
i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
/**
* 这个更好理解,i >>> 4表示往右移动了4位,然后在与i相加,相当于每8位一组,然后8位中的高4位与低4位相加储存在低4位中,
* 然后这里在与0x0f0f0f0f进行与运算,把高4位完全置为0了,因为0x0f0f0f0f用二进制表示就是00001111000011110000111100001111,
* 看到这里可能有些困惑,这里为什么要与0x0f0f0f0f进行与运算,因为每8位一组的话,最多也就是8,那么4位数足够了,高4位就没有必要了,
* 如果不置为0有没有影响,其实如果1的位数极少的话是没什么影响的,但如果1的位数比较多到后面计算的结果可能就会往前进位,导致结果错误,
* 所以这一步要进行一次与运算,那为什么上面的那行代码没有把4位一组中的高两位置0,这是因为4位一组最多有4个1,而2位二进制数最多表示3,
* 小于4,所以不能置为0,
*
*/
i = (i + (i >>> 4)) & 0x0f0f0f0f;
/**
* 和上面类似,每16位分为一组,每组中的高8位和低8位相加,这里的代码相加的很干净,因为无论是高8位还是低8位中的前4位在上面一行中
* 都已经置为0了,这里也可以像上面那样,加完之后在与0x00ff00ff进行与运算,但其实这里已经没有必要了,因为int类型为32位,
* 最多也就32个1,用8位数储存足够了,所以不会超过8位,也就不用担心超过8位在往前进1位的问题了。
*/
i = i + (i >>> 8);
/**
* 和上面类似,就不在详述
*/
i = i + (i >>> 16);
/**
* 到最后为什么要和0x3f进行与运算,0x3f用二进制表示就是111111,因为上面两行没有进行与运算,所以前面的数据都是无效的,
* 只有最后8位是有效的,而后8位的前两位不用说肯定为0,因为最多也就32个1,用后面6位数表示就已经足够了,所以这里与0x3f
* 进行与运算,来计算出最终1的个数
*/
return i & 0x3f;
}
再来看一下java中的bitCount(int var0)的方法
1
2
3
4
5
6
7
8
public static int bitCount(int var0) {
var0 -= var0 >>> 1 & 1431655765;
var0 = (var0 & 858993459) + (var0 >>> 2 & 858993459);
var0 = var0 + (var0 >>> 4) & 252645135;
var0 += var0 >>> 8;
var0 += var0 >>> 16;
return var0 & 63;
}
其实他和Android中的bitCount是一样的,只不过他是10进制,而Android中的是16进制。我们再来看Android中的下一个方法
highestOneBit
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
* Returns an {@code int} value with at most a single one-bit, in the
* position of the highest-order ("leftmost") one-bit in the specified
* {@code int} value. Returns zero if the specified value has no
* one-bits in its two's complement binary representation, that is, if it
* is equal to zero.
*
* @return an {@code int} value with a single one-bit, in the position
* of the highest-order one-bit in the specified value, or zero if
* the specified value is itself equal to zero.
* @since 1.5
*/
public static int highestOneBit(int i) {
// HD, Figure 3-1
i |= (i >> 1);
i |= (i >> 2);
i |= (i >> 4);
i |= (i >> 8);
i |= (i >> 16);
return i - (i >>> 1);
}
他表示的就是从左往右数,遇到第一个1保留,则其之后的所有全部清零,我可以这样来理解,就是小于或等于这个数的最大的2的n次方,当i等于2的n次方的时候,结果还是等于i,当i不是2的n次方的时候就会返回小于i的最大的2的n次方,举个例子,如果i是8则返回8,因为8是2的3次方,如果i是31,则返回16,因为2的4次方是16小于31,而2的5次方是32,大于31,所以32不合适。说到这里,自然会联想到之前写的Android HashMap源码详解中讲到的roundUpToPowerOfTwo(int i)方法,而roundUpToPowerOfTwo方法返回的是大于或等于i的最小的2的n次方。highestOneBit的原理其实很简单,他就是通过左边遇到第一个1然后不停的右移然后在进行与运算,把1后面全部置为1,最后一步在通过i - (i »> 1)把左边第一个1之后的全部置为0,这个可以参照一下roundUpToPowerOfTwo的原理图,大家可以这样理解,当i是2的n次方的时候highestOneBit函数和roundUpToPowerOfTwo函数返回的结果是一样的,当i不是2的n次方的时候,roundUpToPowerOfTwo返回的结果是highestOneBit的2倍。其实讲到这就已经基本上结束了,但由于好奇又看了一下HashMap中初始化数组大小的方法,发现又变了,不得不感慨Android的源码变化实在是太快了,这次看的是Android-25的,代码如下
roundUpToPowerOf2
1
2
3
4
5
6
7
8
9
10
private static int roundUpToPowerOf2(int number) {
// assert number >= 0 : "number must be non-negative";
int rounded = number >= MAXIMUM_CAPACITY
? MAXIMUM_CAPACITY
: (rounded = Integer.highestOneBit(number)) != 0
? (Integer.bitCount(number) > 1) ? rounded << 1 : rounded
: 1;
return rounded;
}
我们看到他已经换成Integer的highestOneBit方法了,我们看到有这样一段代码(Integer.bitCount(number) > 1),他表示number是不是2的n次方,如果是就返回rounded,如果不是就返回rounded«1,因为我们知道highestOneBit是返回小于或等于number的最大的2的n次方,而HashMap初始化的大小是不能小于number的,所以当number为2的n次方的时候直接返回,当number不为2的n次方的时候就会返回rounded的2倍。而java中的highestOneBit和Android中的highestOneBit方法基本类似,这里就不在贴出,下面再来看下一个方法,
reverse
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
* Returns the value obtained by reversing the order of the bits in the
* two's complement binary representation of the specified {@code int}
* value.
*
* @return the value obtained by reversing order of the bits in the
* specified {@code int} value.
* @since 1.5
*/
public static int reverse(int i) {
// HD, Figure 7-1
i = (i & 0x55555555) << 1 | (i >>> 1) & 0x55555555;
i = (i & 0x33333333) << 2 | (i >>> 2) & 0x33333333;
i = (i & 0x0f0f0f0f) << 4 | (i >>> 4) & 0x0f0f0f0f;
i = (i << 24) | ((i & 0xff00) << 8) |
((i >>> 8) & 0xff00) | (i >>> 24);
return i;
}
他表示把i转化为二进制数,然后再把这个二进制数反转,只要把上面的16进制数转化为二进制就一目了然了,我们先来看一下字母的反转,再来分析上面的就容易多了
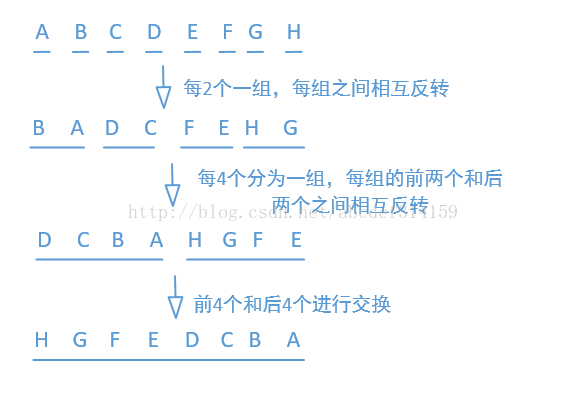
| 看完这个图之后,那么上面的代码就非常容易理解了,先看第一行(i & 0x55555555) « 1 | (i »> 1) & 0x55555555;先把0x55555555转化为二进制,会发现(i & 0x55555555) « 1表示把i的偶数为置0,奇数位不变,然后在左移,把原来的奇数位变成了现在的偶数位,而原来的偶数位变为现在的奇数位,然后全部置为0了,(i »> 1) & 0x55555555右移一位,把原来的偶数为变为奇数位了,然后在与0x55555555进行与运算,相当于把原来的奇数位放到现在的偶数位上,然后全部置为0,原来的偶数位不变然后放到现在的奇数位上,最后来一个 | (或)运算,就相当于把原来的奇偶位交换了。而(i & 0x33333333) « 2 | (i »> 2) & 0x33333333表示每4个一组,然后每组的前后两个进行交换,同理(i & 0x0f0f0f0f) « 4 | (i »> 4) & 0x0f0f0f0f表示每8个一组,然后每组的前4个和后4个进行交换。关键来看最后一行(i « 24) | ((i & 0xff00) « 8) | ((i »> 8) & 0xff00) | (i »> 24),因为前面已经交换到每8个一组了,所以到这里也是每8个分为一组,下面还是画个图来理解一下吧 |

OK,下面再来看下一个方法
reverseBytes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
* Returns the value obtained by reversing the order of the bytes in the
* two's complement representation of the specified {@code int} value.
*
* @return the value obtained by reversing the bytes in the specified
* {@code int} value.
* @since 1.5
*/
public static int reverseBytes(int i) {
return ((i >>> 24) ) |
((i >> 8) & 0xFF00) |
((i << 8) & 0xFF0000) |
((i << 24));
}
| 这个和上面分析的i = (i « 24) | ((i & 0xff00) « 8) | ((i »> 8) & 0xff00) | (i »> 24);其实是一样的,他表示反转字节,因为每个字节占8位,所以每次移动8位。接着往下看 |
numberOfTrailingZeros
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
* Returns the number of zero bits following the lowest-order ("rightmost")
* one-bit in the two's complement binary representation of the specified
* {@code int} value. Returns 32 if the specified value has no
* one-bits in its two's complement representation, in other words if it is
* equal to zero.
*
* @return the number of zero bits following the lowest-order ("rightmost")
* one-bit in the two's complement binary representation of the
* specified {@code int} value, or 32 if the value is equal
* to zero.
* @since 1.5
*/
public static int numberOfTrailingZeros(int i) {
// HD, Figure 5-14
int y;
if (i == 0) return 32;
int n = 31;
y = i <<16; if (y != 0) { n = n -16; i = y; }
y = i << 8; if (y != 0) { n = n - 8; i = y; }
y = i << 4; if (y != 0) { n = n - 4; i = y; }
y = i << 2; if (y != 0) { n = n - 2; i = y; }
return n - ((i << 1) >>> 31);
}
他表示返回从右边数第一个1右边0的个数,如果i是12,则返回2,因为12的二进制是1100,右边有2个0,如果i是0,则返回32,还是在代码里分析效果要好一些
numberOfTrailingZeros
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public static int numberOfTrailingZeros(int i) {
// HD, Figure 5-14
int y;
//等于0的时候返回32
if (i == 0) return 32;
//因为返回的是右边第一个1的右边的0的个数,如果不是0,则0的个数肯定不会大于31
int n = 31;
/**
* 左移16位,如果y==0,说明原来i的低16位上是没有1的,只能说明高16位上有1,那么n肯定是大于或等于16。
* 如果y!=0,说明原来i的低16位上肯定是有1,那么n就会小于16,只需要运算低16就行了,所以就把y赋值给i,
* 同时n也要减去16,
*/
y = i <<16; if (y != 0) { n = n -16; i = y; }
//同上
y = i << 8; if (y != 0) { n = n - 8; i = y; }
//同上
y = i << 4; if (y != 0) { n = n - 4; i = y; }
//同上
y = i << 2; if (y != 0) { n = n - 2; i = y; }
/**
* (i << 1) >>> 31表示计算i的第31位上的值,i << 1表示把i的第31位变成32位,然后再无符号的右移31位,
所以得到的结果就是i的第31位上的值,但是要记住这个i不是最初的那个i,而是运算之后的i,因为上面有赋值,
当满足条件的时候i就会改变。这里为什么要减去第31位上的值,这是因为上面最后一行运行之前其实i已经
判断了(16+8+4=28)位了,当上面最后一行运行之后就只剩下最后两位了,我们知道通过上面一步步的运算,
到这里i的第32位和31位至少有1个1,不可能全是0,如果全是0只有当最初始的i为0的时候,那么这是不可能的,
因为如果最初始的i为0,在最上面就已经被拦截了,直接返回32了。这里为什么要减去31位上的值而不是32位上的值,
这就是算法的巧妙之处,因为这个方法返回的是右边第一个1右边0的个数,所以这里只需要判断第31位就行了,因为如果
31位为1的话,那么32位就没他什么事了,不管他是0还是1都不会有影响,因为31位是在32位的右边(最右边是第一位,
最左边是第32位),只需要把31位的1减掉就行了,如果31位是0,那么32位肯定为1,因为31和32位必须有一个是1,
,其实他这里是把代码简化了,还可以这样写,把最后一行注释掉,改为下面这样,运算结果是一样的
// y = i << 1; if (y != 0) { n = n - 1; }
// return n ;
*/
return n - ((i << 1) >>> 31);
}
还有一个和他类似的方法,我们可以看一下
numberOfLeadingZeros
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
* Returns the number of zero bits preceding the highest-order
* ("leftmost") one-bit in the two's complement binary representation
* of the specified {@code int} value. Returns 32 if the
* specified value has no one-bits in its two's complement representation,
* in other words if it is equal to zero.
*
* <p>Note that this method is closely related to the logarithm base 2.
* For all positive {@code int} values x:
* <ul>
* <li>floor(log<sub>2</sub>(x)) = {@code 31 - numberOfLeadingZeros(x)}
* <li>ceil(log<sub>2</sub>(x)) = {@code 32 - numberOfLeadingZeros(x - 1)}
* </ul>
*
* @return the number of zero bits preceding the highest-order
* ("leftmost") one-bit in the two's complement binary representation
* of the specified {@code int} value, or 32 if the value
* is equal to zero.
* @since 1.5
*/
public static int numberOfLeadingZeros(int i) {
// HD, Figure 5-6
if (i == 0)
return 32;
int n = 1;
if (i >>> 16 == 0) { n += 16; i <<= 16; }
if (i >>> 24 == 0) { n += 8; i <<= 8; }
if (i >>> 28 == 0) { n += 4; i <<= 4; }
if (i >>> 30 == 0) { n += 2; i <<= 2; }
n -= i >>> 31;
return n;
}
这个是返回左边开始连续的为0的个数,这个可以参照上面一个,就不在详细分析,我们可以看到最后一行减去的是运算到最后i的第32位,和上面一个正好相反,因为这个方法返回的是左边开始0的个数。下面再看另一个方法
signum
1
2
3
4
5
6
7
8
9
10
11
12
/**
* Returns the signum function of the specified {@code int} value. (The
* return value is -1 if the specified value is negative; 0 if the
* specified value is zero; and 1 if the specified value is positive.)
*
* @return the signum function of the specified {@code int} value.
* @since 1.5
*/
public static int signum(int i) {
// HD, Section 2-7
return (i >> 31) | (-i >>> 31);
}
这个很简单吧,看名字就知道什么意思,判断符号,正数返回1,负数返回-1,0返回0。如果i是正数,那么i » 31肯定为0,-i为负数,-i »> 31无符号右移,肯定为1,所以结果为1。当i为0的时候结果为0,这个就不在分析。当i为负数的时候,i » 31结果为……1111(共32个1),-i »> 31无论结果是什么,最终结果都是……1111(32个1),他是-1的补码,所以结果为-1。接着往下看
rotateRight
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
* Returns the value obtained by rotating the two's complement binary
* representation of the specified {@code int} value right by the
* specified number of bits. (Bits shifted out of the right hand, or
* low-order, side reenter on the left, or high-order.)
*
* <p>Note that right rotation with a negative distance is equivalent to
* left rotation: {@code rotateRight(val, -distance) == rotateLeft(val,
* distance)}. Note also that rotation by any multiple of 32 is a
* no-op, so all but the last five bits of the rotation distance can be
* ignored, even if the distance is negative: {@code rotateRight(val,
* distance) == rotateRight(val, distance & 0x1F)}.
*
* @return the value obtained by rotating the two's complement binary
* representation of the specified {@code int} value right by the
* specified number of bits.
* @since 1.5
*/
public static int rotateRight(int i, int distance) {
return (i >>> distance) | (i << -distance);
}
他表示循环右移指定位数,移除的不是舍去,而是补到左边,举个例子
1
2
3
4
for (int i = 0; i < 100; i++) {
System.out.println(buwei(Integer.toBinaryString(i)) + "===" + buwei(Integer.toBinaryString(Integer
.rotateRight(i, 4))));
}
看一下打印结果

只截取了前面的几个,他表示往右移动4位,移除的填充到左边。代码很好理解,如果distance为正数,i « -distance表示往左边移动(32-distance)位,i »> distance表示往右边无符号移动distance位,还有另一个类似的方法
rotateLeft
1
2
3
public static int rotateLeft(int i, int distance) {
return (i << distance) | (i >>> -distance);
}
这个和上面一个相反,就不在详述,接着往下看
lowestOneBit
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
* Returns an {@code int} value with at most a single one-bit, in the
* position of the lowest-order ("rightmost") one-bit in the specified
* {@code int} value. Returns zero if the specified value has no
* one-bits in its two's complement binary representation, that is, if it
* is equal to zero.
*
* @return an {@code int} value with a single one-bit, in the position
* of the lowest-order one-bit in the specified value, or zero if
* the specified value is itself equal to zero.
* @since 1.5
*/
public static int lowestOneBit(int i) {
// HD, Section 2-1
return i & -i;
}
这个返回的是从右边起遇到第一个1保留,其他的全部置为0,他和highestOneBit正好相反,highestOneBit表示从左边起遇到第一个1,其他位全部置0。代码很简洁。关于算法的基本上已经分析完了,下面来看一个重量级的类
IntegerCache
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
* Cache to support the object identity semantics of autoboxing for values between
* -128 and 127 (inclusive) as required by JLS.
*
* The cache is initialized on first usage. The size of the cache
* may be controlled by the -XX:AutoBoxCacheMax=<size> option.
* During VM initialization, java.lang.Integer.IntegerCache.high property
* may be set and saved in the private system properties in the
* sun.misc.VM class.
*/
private static class IntegerCache {
static final int low = -128;
static final int high;
static final Integer cache[];
static {
// high value may be configured by property
int h = 127;
String integerCacheHighPropValue =
sun.misc.VM.getSavedProperty("java.lang.Integer.IntegerCache.high");
if (integerCacheHighPropValue != null) {
int i = parseInt(integerCacheHighPropValue);
i = Math.max(i, 127);
// Maximum array size is Integer.MAX_VALUE
h = Math.min(i, Integer.MAX_VALUE - (-low) -1);
}
high = h;
cache = new Integer[(high - low) + 1];
int j = low;
for(int k = 0; k < cache.length; k++)
cache[k] = new Integer(j++);
}
private IntegerCache() {}
}
他里面有个cache数组,缓存了-128到127共256Integer对象,每次创建Integer对象的时候,如果值为-128到127,就会从缓存中取,否则就会重新new一个,看一段代码
1
2
3
4
5
6
Integer i1=120;
Integer i2=120;
Integer i3=130;
Integer i4=130;
System.out.println(i1==i2);
System.out.println(i3==i4);
再来看一下运行结果

结果完全意料之中,因为i1和i2为120,小于127,从缓存中取,是同一对象,而i3和i4大于127,所以创建的是两个不同的对象。接着往下看
valueOf
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
* Returns an {@code Integer} instance representing the specified
* {@code int} value. If a new {@code Integer} instance is not
* required, this method should generally be used in preference to
* the constructor {@link #Integer(int)}, as this method is likely
* to yield significantly better space and time performance by
* caching frequently requested values.
*
* This method will always cache values in the range -128 to 127,
* inclusive, and may cache other values outside of this range.
*
* @param i an {@code int} value.
* @return an {@code Integer} instance representing {@code i}.
* @since 1.5
*/
public static Integer valueOf(int i) {
assert IntegerCache.high >= 127;
if (i >= IntegerCache.low && i <= IntegerCache.high)
return IntegerCache.cache[i + (-IntegerCache.low)];
return new Integer(i);
}
从注释中也可以看到如果i的范围是-128到127,那么就从缓存中取,否则就new一个。接着decode(String nm)代码很简单就不在分析。另外有两个常用的方法toBinaryString和toHexString分别表示转化为二进制字符串和16进制字符串,其实调用的都是同一个方法toUnsignedString(int i, int shift),他表示将Integer转化为无符号字符串,来看一下
toUnsignedString
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
private static String toUnsignedString(int i, int shift) {
//int类型总共32位
char[] buf = new char[32];
int charPos = 32;
//radix基数,如果是二进制radix为2,如果是16进制radix就为16,一般为2的n次方
int radix = 1 << shift;
//这个在讲到HashMap的时候说过,2的n次方减去1则后面全为1,原来为1的位置及之前全为0.
int mask = radix - 1;
do {
//存到数组中
buf[--charPos] = digits[i & mask];
//偏移量,这里很好理解,因为Integer是32位,如果shift为3就是八进制,为4就是16进制,这里偏移就是按照多少进制来偏移的。
i >>>= shift;
} while (i != 0);
return new String(buf, charPos, (32 - charPos));
}
代码很简单,就不在详细介绍。记得以前经常会有这样的烦恼,就是如果我打印二进制的时候我要求必须打印32位,因为这样好进行比较,但实际情况不是这样,但可以把上面代码改一下达到要求
toUnsignedString
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private static String toUnsignedString(int i, int shift) {
//int类型总共32位
char[] buf = new char[32];
Arrays.fill(buf, '0');//增加
int charPos = 32;
//radix基数,如果是二进制radix为2,如果是16进制radix就为16,一般为2的n次方
int radix = 1 << shift;
//这个在讲到HashMap的时候说过,2的n次方减去1则后面全为1,原来为1的位置及之前全为0.
int mask = radix - 1;
do {
//存到数组中
buf[--charPos] = digits[i & mask];
//偏移量
i >>>= shift;
} while (i != 0);
//return new String(buf, charPos, (32 - charPos));
return new String(buf, 0, 32);//修改
}
我们看一下
1
2
3
for (int i = -100; i <100 ; i++) {
System.out.println(toUnsignedString(i,1));
}
再看一下运行结果,我从中间截取一部分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11111111111111111111111111110111
11111111111111111111111111111000
11111111111111111111111111111001
11111111111111111111111111111010
11111111111111111111111111111011
11111111111111111111111111111100
11111111111111111111111111111101
11111111111111111111111111111110
11111111111111111111111111111111
00000000000000000000000000000000
00000000000000000000000000000001
00000000000000000000000000000010
00000000000000000000000000000011
00000000000000000000000000000100
00000000000000000000000000000101
00000000000000000000000000000110
我们看到每个都是32位。
1
2
3
4
5
6
7
8
9
final static int [] sizeTable = { 9, 99, 999, 9999, 99999, 999999, 9999999,
99999999, 999999999, Integer.MAX_VALUE };
// Requires positive x
static int stringSize(int x) {
for (int i=0; ; i++)
if (x <= sizeTable[i])
return i+1;
}
stringSize(int x)表示的x是几位数。0到9是一位数,10到99是两位数……。接下来看一下getChars(int i, int index, char[] buf)函数,他表示把i提取到buf中,index是buf的长度,通过DigitTens和DigitOnes可以看到i是转化为10进制的。这个函数比较复杂,打算在代码中分析
getChars
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
* Places characters representing the integer i into the
* character array buf. The characters are placed into
* the buffer backwards starting with the least significant
* digit at the specified index (exclusive), and working
* backwards from there.
*
* Will fail if i == Integer.MIN_VALUE
*/
//从注释中可以看出,如果i==Integer.MIN_VALUE,这个方法将失效。
static void getChars(int i, int index, char[] buf) {
int q, r;
int charPos = index;
char sign = 0;//表示符号位
if (i < 0) {
sign = '-';
i = -i;//如果i为负数,变为正数。
}
// Generate two digits per iteration
while (i >= 65536) {//当大于65536的时候每两位开始操作
q = i / 100;
// really: r = i - (q * 100);
//r是i对100求余的结果,相当于r=i%100;为什么不这样写,我个人认为应该是效率问题,通过移位操作效率要高一些,
//((q << 6) + (q << 5) + (q << 2))相当于q*64+q*32+q*4也就是q*100;
r = i - ((q << 6) + (q << 5) + (q << 2));
i = q;
//把数字存储到数组中,注意这个数组是从后往前存放的,如果仔细查看DigitTens和DigitOnes,可以发现DigitOnes[r]其实相当于DigitOnes[r%10],
//DigitTens[r]其实相当于DigitTens[r/10]
buf [--charPos] = DigitOnes[r];
buf [--charPos] = DigitTens[r];
}
// Fall thru to fast mode for smaller numbers
// assert(i <= 65536, i);
for (;;) {
//这里2^19=524288,(i * 52429) >>> (16+3)等于52429/524288=0.1000003814697266,相当于i除以10.因为乘法和移位的效率要高于除法,
//至于上面的为什么没有使用乘法和移位,是因为当i大于65536的时候在乘法容易溢出,这里为什么要选择19,待会在下面再看
q = (i * 52429) >>> (16+3);
//求余,相当于r=i-q*10;上面的q约等于i/10;
r = i - ((q << 3) + (q << 1)); // r = i-(q*10) ...
buf [--charPos] = digits [r];//存放到数组中。
i = q;
if (i == 0) break;
}
if (sign != 0) {//如果i为负数,把负号添加到buf的前面,切记buf是从后往前添加的
buf [--charPos] = sign;
}
}
下面来看一下上面为什么选择19的问题,我写了一段代码
calculate
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private static void calculate() {
// 相乘的数不能比max大,否则当i接近65536的时候会出现Integer溢出,
int max = (int) (Integer.MAX_VALUE * 1.0 / (1 << 16) * 10);// 1<<16相当于65536;
int j = 0;// 移动j位接近max
int t = 1;// 临时变量,主要用于计算j的值。
while (t < max) {
t = (t << 1);
j++;
}
// 最大移动位j,当1移动j位时相当于调用 highestOneBit(int i)函数。
for (int m = 1; m <= j; m++) {
int k = 1 << m;
int mole = k % 10;
int q = k / 10;
if (mole >= 5)// 四舍五入
q++;
System.out.println(m + "→→→→" + q * 1.0d / k);
}
}
上面都有注释,很简单就不在介绍,下面看一下运行结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
1
0
1→→→→0.0
2→→→→0.0
3→→→→0.125
4→→→→0.125
5→→→→0.09375
6→→→→0.09375
7→→→→0.1015625
8→→→→0.1015625
9→→→→0.099609375
10→→→→0.099609375
11→→→→0.10009765625
12→→→→0.10009765625
13→→→→0.0999755859375
14→→→→0.0999755859375
15→→→→0.100006103515625
16→→→→0.100006103515625
17→→→→0.09999847412109375
18→→→→0.09999847412109375
19→→→→0.10000038146972656
我们看到当i越大的时候,结果越接近于0.1.所以选择i等于19.下面再看另一个方法toString(int i),代码也很简单,就简单介绍一下
toString
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/**
* Returns a {@code String} object representing the
* specified integer. The argument is converted to signed decimal
* representation and returned as a string, exactly as if the
* argument and radix 10 were given as arguments to the {@link
* #toString(int, int)} method.
*
* @param i an integer to be converted.
* @return a string representation of the argument in base 10.
*/
public static String toString(int i) {
if (i == Integer.MIN_VALUE)
return "-2147483648";
// Android-changed: cache the string literal for small values.
boolean negative = i < 0;//判断是否是负数
boolean small = negative ? i > -100 : i < 100;
if (small) {//如果i大于等于-100并且小于等于100,则从缓存中取
final String[] smallValues = negative ? SMALL_NEG_VALUES : SMALL_NONNEG_VALUES;
if (negative) {
i = -i;
if (smallValues[i] == null) {//如果缓存为空则创建
smallValues[i] =
i < 10 ? new String(new char[]{'-', DigitOnes[i]})
: new String(new char[]{'-', DigitTens[i], DigitOnes[i]});
}
} else {
if (smallValues[i] == null) {//如果缓存为空则创建
smallValues[i] =
i < 10 ? new String(new char[]{DigitOnes[i]})
: new String(new char[]{DigitTens[i], DigitOnes[i]});
}
}
return smallValues[i];
}
//如果不是在缓存的范围之内,则调用getChars方法,看到下面如果为负数时,size会加1,因为在getChars的最后两行要判断符号位的
int size = negative ? stringSize(-i) + 1 : stringSize(i);
char[] buf = new char[size];
getChars(i, size, buf);
// Android-changed: change string constructor.
return new String(buf);
}
还有一个类似的toString(int i, int radix)方法,不过上面返回的是十进制的,这个可以根据传的进制参数返回,比上一个要智能,看一下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public static String toString(int i, int radix) {
//如果radix小于2或者大于36,则返回10进制。Character.MIN_RADIX为2,Character.MAX_RADIX是36
// public static final int MAX_RADIX = 36;
if (radix < Character.MIN_RADIX || radix > Character.MAX_RADIX)
radix = 10;
/* Use the faster version */
if (radix == 10) {//如果十进制调用上一个方法
return toString(i);
}
char buf[] = new char[33];
boolean negative = (i < 0);
int charPos = 32;
if (!negative) {// 如果不为负数,让i变为负数。
i = -i;
}
while (i <= -radix) {
int q = i / radix;
//这里radix * q - i相当于对i求余,如果理解不了可以把radix想象为10进制估计就好一些了
buf[charPos--] = digits[radix * q - i];
i = q;
}
buf[charPos] = digits[-i];
if (negative) {// 如果为负数添加负号
buf[--charPos] = '-';
}
return new String(buf, charPos, (33 - charPos));
}
下面再看最后一个方法parseInt
parseInt
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
public static int parseInt(String s, int radix)
throws NumberFormatException
{
/*
* WARNING: This method may be invoked early during VM initialization
* before IntegerCache is initialized. Care must be taken to not use
* the valueOf method.
*/
if (s == null) {
throw new NumberFormatException("null");
}
if (radix < Character.MIN_RADIX) {
throw new NumberFormatException("radix " + radix +
" less than Character.MIN_RADIX");
}
if (radix > Character.MAX_RADIX) {
throw new NumberFormatException("radix " + radix +
" greater than Character.MAX_RADIX");
}
int result = 0;// 根据最后一行的判断,result保存的是负数.
boolean negative = false;//判断是否是负数
int i = 0, len = s.length();
int limit = -Integer.MAX_VALUE;//正数的极限值
int multmin;
int digit;
if (len > 0) {
char firstChar = s.charAt(0);
//这里主要判断如果是负数的操作。
if (firstChar < '0') { // Possible leading "+" or "-"
if (firstChar == '-') {// 是负数
negative = true;
limit = Integer.MIN_VALUE;//如果是负数,则极限值是Integer.MIN_VALUE
} else if (firstChar != '+')//如果小于0,并且既不是"-"又不是"+"直接抛异常
throw NumberFormatException.forInputString(s);
if (len == 1) // Cannot have lone "+" or "-"//如果只是一个符号也抛异常
throw NumberFormatException.forInputString(s);
i++;
}
multmin = limit / radix;
while (i < len) {
// Accumulating negatively avoids surprises near MAX_VALUE
digit = Character.digit(s.charAt(i++),radix);
if (digit < 0) {//数字不能小于0
throw NumberFormatException.forInputString(s);
}
if (result < multmin) {//如果不判断,下面相乘会出现溢出,超过极限值,为什么要用小于,是因为result和multmin都是负数,
throw NumberFormatException.forInputString(s);
}
//逐个取出每一个字符与radix相乘,radix表示进制,比如2,8,10,10等,如果还是不好理解,就把radix想象为10进制吧。
result *= radix;
if (result < limit + digit) {//这里为什么要这样判断,是因为limit是负数,digit是正数,防止下面的操作导致结果溢出
throw NumberFormatException.forInputString(s);
}
result -= digit;//注意这里为什么要减,因为result是负数,在最后才进行符号判断
}
} else {
throw NumberFormatException.forInputString(s);
}
return negative ? result : -result;//如果知道result是负数,这里就好理解了
}
OK,到现在为止Integer的所有方法基本都已分析完毕