“相逢不饮空归去，洞口桃花也笑人。”
正文
在分析源代码之前，最好要标注出处，因为在Java中和Android中同一个类可能代码就会不一样，甚至在Android中不同版本之间代码也可能会有很大的差别，下面分析的是红黑树TreeMap，在\sources\android-25中。
红黑树的几个性质要先说一下，
性质
1.每个节点是红色或者黑色的。
2.根节点是黑色的。
3.每个叶节点的子节点是黑色的（叶子节点的子节点可以认为是null的）。
4.如果一个节点是红色的，则它的左右子节点都必须是黑色的。
5.对任意一个节点来说，从它到叶节点的所有路径必须包含相同数目的黑色节点。
TreeMap还有一个性质，就是他的左子树比他小，右子树比他大，这里的比较是按照key排序的。存放的时候如果key一样就把他替换了。
乍一看代码TreeMap有3000多行，其实他里面有很多内部类，有Values,EntrySet,KeySet,PrivateEntryIterator,EntryIterator,ValueIterator,KeyIterator,DescendingKeyIterator, NavigableSubMap,AscendingSubMap,DescendingSubMap,SubMap,TreeMapEntry,TreeMapSpliterator, KeySpliterator,DescendingKeySpliterator,ValueSpliterator,EntrySpliterator多达十几个内部类。其实很多都不需要了解，下面主要来看一下TreeMapEntry这个类，它主要是红黑树的节点
TreeMapEntry
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
/**
* Node in the Tree. Doubles as a means to pass key-value pairs back to
* user (see Map.Entry).
*/
static final class TreeMapEntry<K,V> implements Map.Entry<K,V> {
K key;
V value;
TreeMapEntry<K,V> left = null;//左子树
TreeMapEntry<K,V> right = null;//右子树
TreeMapEntry<K,V> parent;//父节点
boolean color = BLACK;//默认为黑色
/**
* Make a new cell with given key, value, and parent, and with
* {@code null} child links, and BLACK color.
*/
TreeMapEntry(K key, V value, TreeMapEntry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* Returns the key.
*
* @return the key
*/
public K getKey() {
return key;
}
/**
* Returns the value associated with the key.
*
* @return the value associated with the key
*/
public V getValue() {
return value;
}
/**
* Replaces the value currently associated with the key with the given
* value.
*
* @return the value associated with the key before this method was
* called
*/
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}
既然是棵树，那么肯定就会有put方法以及remove方法，那么这里就从最简单的着手，先看一下put方法
put
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
/**
* Associates the specified value with the specified key in this map.
* If the map previously contained a mapping for the key, the old
* value is replaced.
*
* @param key key with which the specified value is to be associated
* @param value value to be associated with the specified key
*
* @return the previous value associated with {@code key}, or
* {@code null} if there was no mapping for {@code key}.
* (A {@code null} return can also indicate that the map
* previously associated {@code null} with {@code key}.)
* @throws ClassCastException if the specified key cannot be compared
* with the keys currently in the map
* @throws NullPointerException if the specified key is null
* and this map uses natural ordering, or its comparator
* does not permit null keys
*/
//注释说的很明白，如果有相同的key，那么之前老的就会被代替，
public V put(K key, V value) {
TreeMapEntry<K,V> t = root;
if (t == null) {
// We could just call compare(key, key) for its side effect of checking the type and
// nullness of the input key. However, several applications seem to have written comparators
// that only expect to be called on elements that aren't equal to each other (after
// making assumptions about the domain of the map). Clearly, such comparators are bogus
// because get() would never work, but TreeSets are frequently used for sorting a set
// of distinct elements.
//
// As a temporary work around, we perform the null & instanceof checks by hand so that
// we can guarantee that elements are never compared against themselves.
//
// compare(key, key);
//
// **** THIS CHANGE WILL BE REVERTED IN A FUTURE ANDROID RELEASE ****
// key检查，如果comparator为null，那么key是不能为null的，并且key是实现Comparable接口的，因为TreeMaori是有序的，需要比较.
//如果comparator不为null，则需要验证，comparator是自己传进来的，根据key == null，comparator.compare(key, key)是否可执行，
//还是抛异常，这个是由你自己写的compare方法决定的。
if (comparator != null) {
if (key == null) {
comparator.compare(key, key);
}
} else {//如果没有传入comparator，则key不能为null，且必须实现Comparable接口
if (key == null) {
throw new NullPointerException("key == null");
} else if (!(key instanceof Comparable)) {
throw new ClassCastException(
"Cannot cast" + key.getClass().getName() + " to Comparable.");
}
}
//创建root，这个是在上面root为null的时候才走到这一步
root = new TreeMapEntry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
TreeMapEntry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
//comparator无论是等于null还是不等于null，原理都是基本差不多
if (cpr != null) {
do {//添加的时候如果原来有就替换，如果没有就不断的循环，这里注意TreeMap的左子树比他小，右子树比他大，这里比较的是key
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)//小的就找左子树
t = t.left;
else if (cmp > 0)//大的就找右子树
t = t.right;
else
return t.setValue(value);//如果正好找到了就把它替换掉
} while (t != null);
}
else {//这个是使用默认的比较器，原理和上面是一样的
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
TreeMapEntry<K,V> e = new TreeMapEntry<>(key, value, parent);//创建一个节点
if (cmp < 0)//节点比他父节点小，放到左子树
parent.left = e;
else
parent.right = e;//节点比他父节点大，放到右子树
fixAfterInsertion(e);
//这里是关键，树的调整，因为上面创建节点的时候默认的是一棵黑色的数，而树原来是平衡的，加入节点之后导致数的不平衡，所以需要调节
size++;
modCount++;
return null;
}
put方法存放的时候，首先是会存放到叶子节点，然后在进行调整。上面有一个重量级的方法fixAfterInsertion还没有分析，在分析fixAfterInsertion方法之前来看一下其他的几个方法，
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
private static <K,V> boolean colorOf(TreeMapEntry<K,V> p) {
//获取树的颜色，如果为null，则为黑色，这一点要记住，待会下面分析的时候会用到
return (p == null ? BLACK : p.color);
}
//找父节点
private static <K,V> TreeMapEntry<K,V> parentOf(TreeMapEntry<K,V> p) {
return (p == null ? null: p.parent);
}
//设置节点颜色
private static <K,V> void setColor(TreeMapEntry<K,V> p, boolean c) {
if (p != null)
p.color = c;
}
//获取左子树
private static <K,V> TreeMapEntry<K,V> leftOf(TreeMapEntry<K,V> p) {
return (p == null) ? null: p.left;
}
//获取右子树
private static <K,V> TreeMapEntry<K,V> rightOf(TreeMapEntry<K,V> p) {
return (p == null) ? null: p.right;
}
下面再来看一下fixAfterInsertion方法
fixAfterInsertion
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/** From CLR */
private void fixAfterInsertion(TreeMapEntry<K,V> x) {
//在红黑树里面，如果加入一个黑色节点，则导致所有经过这个节点的路径黑色节点数量增加1，
//这样就肯定破坏了红黑树中到所有叶节点经过的黑色节点数量一样的约定。所以，
//我们最简单的办法是先设置加入的节点是红色的。
x.color = RED;
//当前节点变为红色，如果他的父节点是红色则需要调整，因为父节点和子节点不能同时为红色，但可以同时为黑色，
//所以这里的循环条件是父节点必须为红色才需要调整。
while (x != null && x != root && x.parent.color == RED) {
//这里会分多钟情况讨论，
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {//如果父节点是爷爷节点的左节点
TreeMapEntry<K,V> y = rightOf(parentOf(parentOf(x)));//当前节点的叔叔节点，也就是他父节点的兄弟节点，这个也可能为null
if (colorOf(y) == RED) {
//因为添加的是红色，而父与子不能同时为红色，所以打破了平衡，需要先让父为黑色，然后再让爷爷为红色，因为爷爷节点为红色，所以
//子节点必须为黑色，所以把叔叔节点也调为黑色，继续往上调整，
//(1)如果当前节点的叔叔节点是红色，也就是说他的叔叔节点一定是存在的，因为如果为null,则colorOf会返回黑色。既然叔叔节点
//是红色，那么他的爷爷节点一定是黑色，否则就打破了红黑平衡，那么他的父节点也一定是红色，因为只有父节点为红色才执行while
//循环，这种情况下，无论x是父节点的左节点还是右节点都不需要在旋转，
setColor(parentOf(x), BLACK);//让x的父节点为黑色
setColor(y, BLACK);//叔叔节点也设为黑色
setColor(parentOf(parentOf(x)), RED);//当前节点的爷爷节点为红色
//把爷爷节点设置为红色之后，继续往上循环，即使执行到最上端也不用担心，因为在最后会把根节点设置为黑色的。
x = parentOf(parentOf(x));
} else {
//如果他的叔叔节点是黑色的，并且他的父节点是红色的，那么说明他的叔叔节点是null，因为如果叔叔节点是黑色的且不为空,
//那么违反了他的第5条性质所以这里叔叔节点是空。因为叔叔节点
//为空，出现了不平衡,所以这里当前节点无论是父节点的左节点还是右节点，都需要旋转
if (x == rightOf(parentOf(x))) {
//(2)当前节点是父节点的右节点，
x = parentOf(x);//让当前节点的父节点为当前节点
rotateLeft(x);//对父节点进行左旋
}
//(3)当前节点是父节点的左节点，这个左节点有可能是添加的时候添加到左节点的，也有可能是上面旋转的时候旋转到左节点的
setColor(parentOf(x), BLACK);//让父节点为黑色
setColor(parentOf(parentOf(x)), RED);//爷爷节点变为红色
rotateRight(parentOf(parentOf(x)));//对爷爷节点右旋
}
} else {//父节点为爷爷节点的右节点
TreeMapEntry<K,V> y = leftOf(parentOf(parentOf(x)));//找出叔叔节点
//如果叔叔节点是红色，那么说明他一定是存在的，所以不需要旋转，这里要铭记，无论是左旋还是右旋的前提条件是他的叔叔节点不存在，
//如果存在就不需要旋转，只需要遍历改变颜色值即可
if (colorOf(y) == RED) {
//(4)修改颜色
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));//改变颜色之后遍历
} else {//没有叔叔节点
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);//(5)右旋操作
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));//(6)左旋操作
}
}
}
root.color = BLACK;//根节点必须是黑色
}
上面列出了6中可能，下面通过6张图来说明 下面是图1，不需要旋转，只需要调整颜色即可
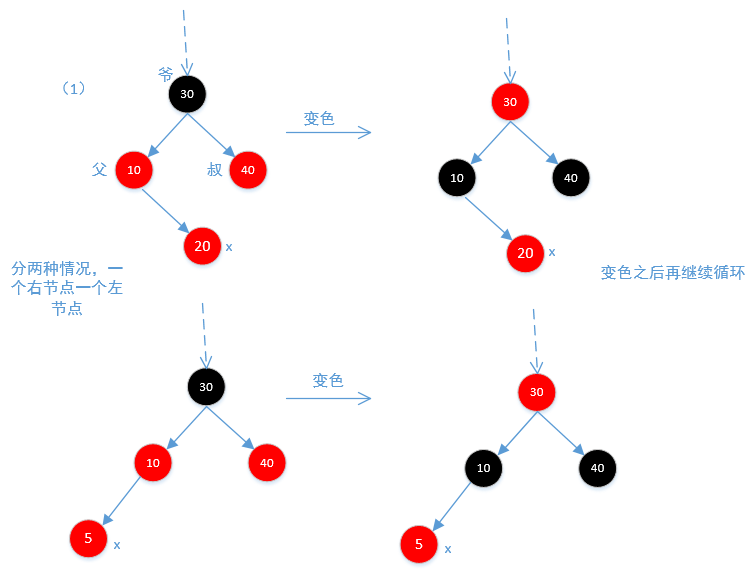下面是图2和图3，因为不平衡，所以需要旋转
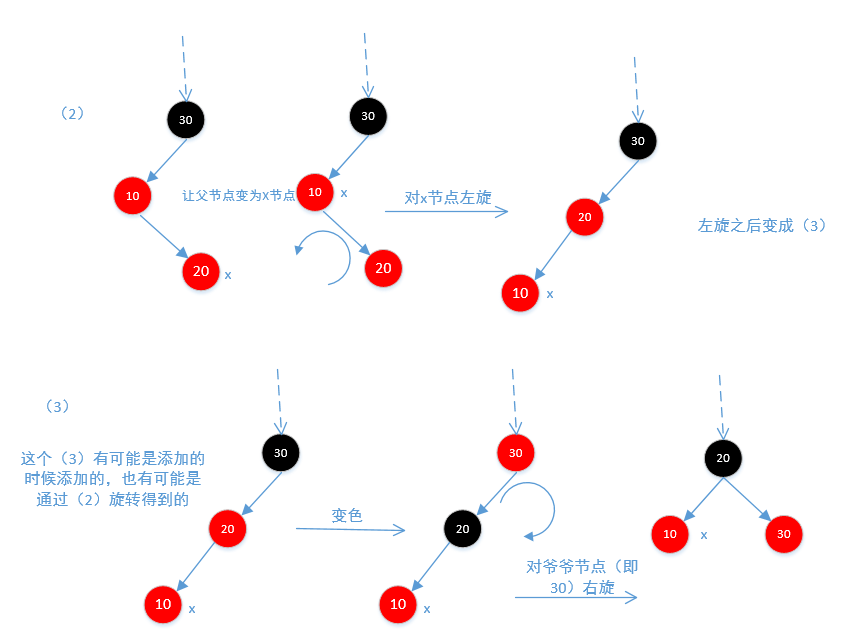
下面是图4，和图1差不多，也分两种情况，一种是左节点一种是右节点
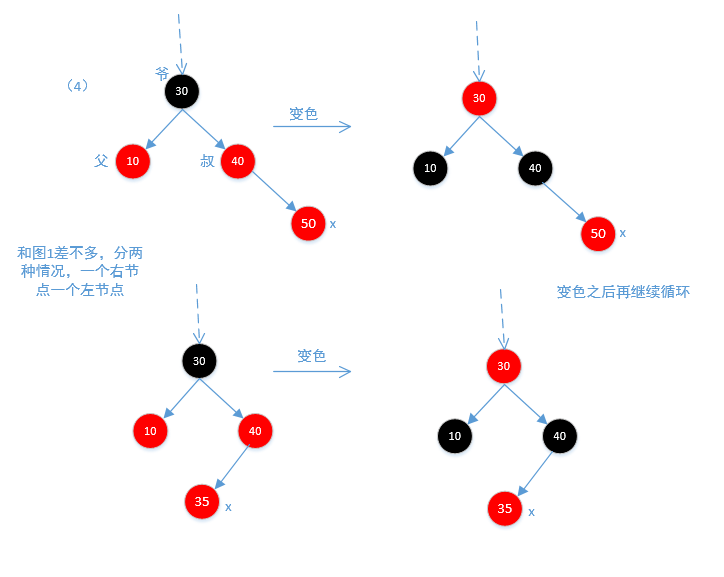
下面是图5和图6，因为不平衡，所以需要旋转
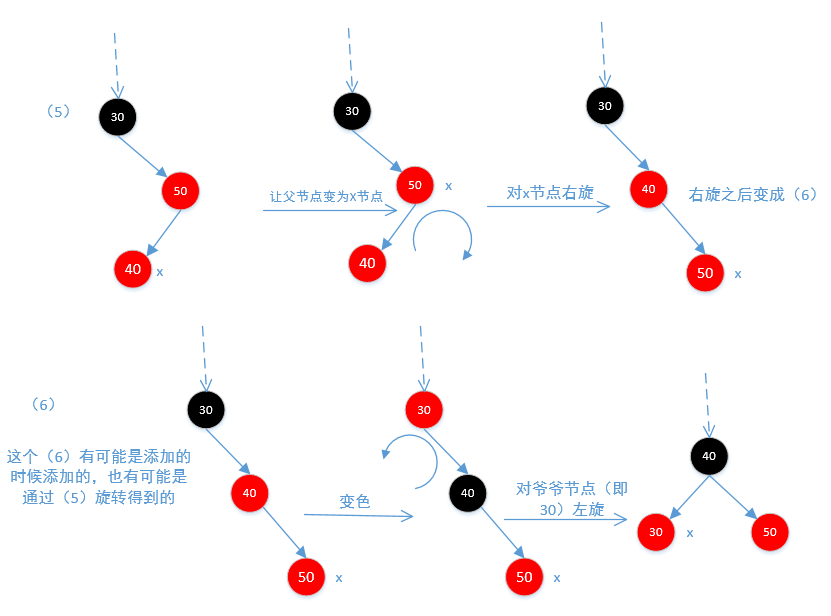无论怎么旋转，他的左节点永远小于他，右节点永远大于他。通过不断的while循环，最终保证红黑树的平衡。下面来看一下旋转的方法，先看一下图
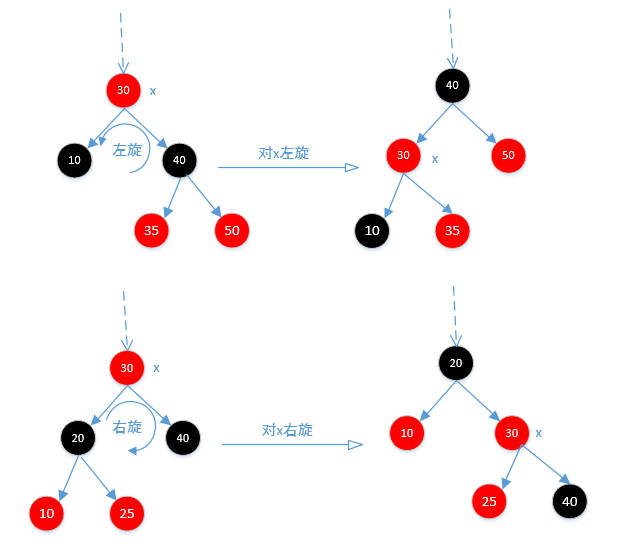
rotateLeft
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/** From CLR */
private void rotateLeft(TreeMapEntry<K,V> p) {
//参照上面旋转的图来分析，p就是图中的x
if (p != null) {
TreeMapEntry<K,V> r = p.right;//r相当于图中的40节点
p.right = r.left;//让35节点（r.left也就是图中40节点的左节点）等于p的右节点，看上图
//如果r.left！=null，让p等于他的父节点，因为在上一步他已经等于p的右节点，自然就是他的子节点
//所以他的父节点自然就变成p了
if (r.left != null)
r.left.parent = p;
//让原来p节点的父节点等于r的父节点，可以根据图看的很明白，通过旋转40节点，挪到上面了，
r.parent = p.parent;
//这里也很好理解，如果原来p的父节点为null，说明原来父节点就是根节点，这里让调整过来的r节点
//（即40节点）成为根节点
if (p.parent == null)
root = r;
//这里很好理解，如果原来p节点是左节点就让调整过来的r节点变成左节点，是右节点就让r变成右节点
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
//让p（也就是图中的30节点）成为r（也就是图中的40节点）的左节点，
r.left = p;
//然后让r（图中的40节点）成为p（图中的30节点）的父节点。
p.parent = r;
}
}
而右旋方法rotateRight和左旋差不多，这里就不在分析。put方法分析完了，那么下一个就是remove方法了，
remove
1
2
3
4
5
6
7
8
9
10
11
12
public V remove(Object key) {
//getEntry(Object key)方法是获取TreeMapEntry，如果比当前节点大则找右节点，如果比当前节点小则找左节点
//通过不断的循环，知道找到为止，如果没找着则返回为null。
TreeMapEntry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
//找到之后删除
deleteEntry(p);
return oldValue;
}
下面再看一下删除方法deleteEntry。
deleteEntry
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
/**
* Delete node p, and then rebalance the tree.
*/
private void deleteEntry(TreeMapEntry<K,V> p) {
modCount++;
size--;//删除，size减1
// If strictly internal, copy successor's element to p and then make p
// point to successor.
//当有两个节点的时候不能直接删除，要删除他的后继节点，后继节点最多只有一个子节点。因为如果p有两个子节点，你删除之后
//他的两个子节点怎么挂载，挂载到p的父节点下？这显然不合理，因为这样一来p的父节点很有可能会有3个子节点，那么最好的办法
//就是找一个替罪羊，删除p的后继节点s，当然删除前需要把后继节点s的值赋给p
if (p.left != null && p.right != null) {
//successor(p)返回p节点的后继节点，其实这个后继节点就是比p大的最小值，这个待会再分析
TreeMapEntry<K,V> s = successor(p);
//把后继节点s的值赋值给p，待会删除的是后继节点s，注意这里赋值并没有把颜色赋给原来的p。当然这里删除并不会打乱树的
//大小顺序，因为后继节点是比p大的最小值，赋值之后在删除，树的大小顺序依然是正确的，这里只是把s的值赋给了p，如果
//再把p原来的值赋给s，在删除s可能就会更好理解了，但这其实并不影响。
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
TreeMapEntry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
//p有子节点，并且有且只有一个节点，因为如果p有两个节点，那么上面的successor方法会一直查找，要么返回p的右节点
//（前提是p的右节点没有左节点），要么会一直循环找到p的右节点的最左孙子节点。待会看successor代码会发现，如果p
//有2个子节点，那么successor返回的节点最多也只有1个节点。
// Link replacement to parent
replacement.parent = p.parent;
//如果p的父节点为null，说明p是root节点，因为执行到这一步，所以replacement是p唯一的节点，把p节点删除后，让
//replacement成为root节点
if (p.parent == null)
root = replacement;
//这个不会变，原来p是左节点就让replacement成为左节点，原来p为右节点就让replacement成为右节点。相当于替换p节点的位置
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
//把p的子节点及父节点全部断开
p.left = p.right = p.parent = null;
// Fix replacement
//如果删除的是黑色要进行调整，因为黑色删除会打破红黑平衡，
//所以这里只是做颜色调整，调整的时候并没有删除。
if (p.color == BLACK)
//上面的p确定只有一个节点replacement，但这里replacement子节点是不确定的，有可能0个，1个或2个。
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;//p是根节点，直接删除，不用调整
} else { // No children. Use self as phantom replacement and unlink.
//p没有子节点，说明p是个叶子节点，不需要找继承者，调整完之后直接删除就可以了。
//如果删除的是黑色，需要调整,上面的调整是删除之后再调整，是因为删除的不是叶子节点，如果调整之后再删除还有可能出现错误，
//而这里是调整之后再删除，是因为这里删除的是叶子节点，调整完之后直接把叶子节点删除就是了，删除之后调整的是颜色，并不是树的
//大小顺序
if (p.color == BLACK)
fixAfterDeletion(p);
//调整完之后再删除p节点，此时p是叶子节点，因为调整完之后通过左旋或右旋p.rarent可能为null，所以这里需要判断
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
上面分析的时候有两个方法successor和fixAfterDeletion没有分析，下面先来看一下successor方法，这个方法很简单，其实就是返回大于节点p的最小值，看一下代码
successor
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
* Returns the successor of the specified Entry, or null if no such.
*/
static <K,V> TreeMapEntry<K,V> successor(TreeMapEntry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) {//t的右节点不为空
TreeMapEntry<K,V> p = t.right;
//循环左节点，如果左节点一开始就为null，那么直接就返回p，此时p是t的右节点，如果p的左节点
//存在，那么会一直循环，一直在找左节点，直到为null为止，
while (p.left != null)
p = p.left;
return p;//所以查找到最后，返回的p最多只有一个节点，并且查找的p是大于t的最小值
} else {
TreeMapEntry<K,V> p = t.parent;
TreeMapEntry<K,V> ch = t;
//不停的往上找父节点，直到p为null，或者父节点（这个父节点也可能是父节点的父节点的父节点，反正
//只要满足条件就会一直往上循环）是左节点，最终查找的结果是p是大于t的最小值，要明白这一点，首先要
//明白，一个节点大于他的左节点小于他的右节点
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;//这里返回的p有可能有2个子节点，并且只有在t没有右节点的时候才有可能。
}
}
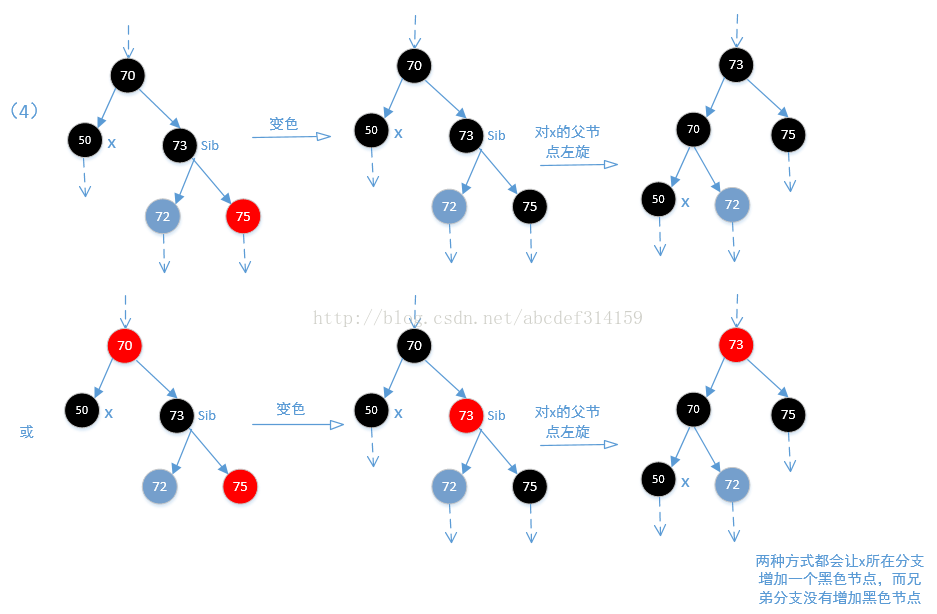
OK，下面再来看一下fixAfterDeletion方法，因为x所在分支少了一个黑色的节点，所以他的主要目的就是让x分支增加一个黑色节点。这个比fixAfterInsertion方法还难理解，看代码
fixAfterDeletion
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
/** From CLR */
private void fixAfterDeletion(TreeMapEntry<K,V> x) {
//再看这个方法之前先看一下最后一行代码，他会把x节点设置为黑色
//很明显，在x只有黑色的时候才会调整，因为删除黑色打破了红黑平衡，但deleteEntry方法中的删除有两种，
//一种是替换之后的replacement，这个replacement不是删除的节点，需要删除的节点在这之前就已经被删除，
//他是来找平衡的，因为删除之后在这一分支上少了一个黑色节点，如果replacement节点为红色，那么不用执行
// while循环，直接在最后把它置为黑色就正好弥补了删除的黑色节点，如果replacement是黑色，那么需要执行
//下面的while循环（前提是replacement不等于root）。还一种就是没有子节点的，先调整完在删除，如果他是
//红色，就不用执行while循环，直接删除就是了，下面置不置为黑色都一样，如果是黑色，就必须执行下面的方法,
//因为删除黑色会打破红黑平衡。
while (x != root && colorOf(x) == BLACK) {
//x是父节点的左节点
if (x == leftOf(parentOf(x))) {
TreeMapEntry<K,V> sib = rightOf(parentOf(x));//x的兄弟节点
//（1）兄弟节点是红色，这种情况下兄弟节点的父节点和子节点都一定是黑色的，
//然后让兄弟节点变为黑色，父节点变为红色，这种情况下从root节点到兄弟节点的各叶子节点黑色个数没有变化，
//但从root节点到x节点的黑色个数少了1（如果删除的是黑色节点，那么传进来的replacement分支上其实就已经少
//了一个黑色，但这里减少只是相对于传进来的x来说的，是相对的。），然后通过左旋，达到各分支上的黑色
//节点一致。
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));//左旋
//通过左旋，x的位置已经改变，但这里sib还是等于x的兄弟节点。
sib = rightOf(parentOf(x));
}
//其实执行到这一步往后可以认为x所在分支少了一个黑色节点。并且兄弟节点sib是黑色的
//（2）首先可以肯定一点的是sib节点肯定是黑色的，通过（1）及上面代码可以明白，如果sib是红色，那么他的子节
//点是黑色的，经过上面的左旋调整，sib的子节点会变为sib，也就是黑色。这里如果sib的两个子节点都是黑色的，那么
//让sib为红色，这样一来x分支和他兄弟分支sib都相当于少了一个黑色节点，所以从root节点到x分支和到sib分支的黑色
//节点都是一样的。那么问题来了，从root节点到x和sib分支的黑色节点比到其他分支的黑色节点明显是少了一个黑色节点，
//但是后面又让x等于x的父节点，所以如果父节点为红色，则跳出循环，在最后再变为黑色，此时所有的节点都又达到平衡，
//如果为黑色，则继续循环。
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
//（3）如果sib的右子节点是黑色，左子节点是红色（如果两个都是黑色则执行上面），这样不能直接让sib节点变为红色，因为
//这样会打破平衡.这个时候需要让左子节点变黑色，sib节点再变为红色。如果这样，那么问题就来了，因为这样从root到
//sib左分支的黑色节点是没有变化，但从root到sib右分支的黑色节点明显是少了一个黑色节点，然后再对sib进行右旋，
//让sib的左右子节点又各自达到平衡。然后在重新定位sib节点。但即使这样，从root到x节点的分支依然少了一个黑色节点。
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
//（4）由上上面可知sib是黑色的，即使sib的右节点为黑色，通过上面的改变颜色及旋转到最后sib还是黑色。sib的右节点是红色，
//如果是黑色，那么执行上面也会变为黑色，可以看一下下面的图（3）.执行到这一步，从root
//到sib分支的黑色节点是没有变化，但从root到x分支的黑色节点是少了一个，然后执行下面的代码会使x的兄弟分支黑色节点不变
//x分支黑色节点加1，最终达到平衡。然后让x等于root，退出循环。最后是对root置为黑色，基本没有影响（因为root节点
//本来就是黑色）,这里的代码让sib的颜色等于x父节点的颜色，基本没影响，其实他最终目的是让x所在分支增加一个黑色节点，
//来达到红黑平衡。
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else { // symmetric
//对称的，x是父节点的右节点的情况。
TreeMapEntry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);//最后把x节点置为黑色
}
结合上面代码看一下下面的四张图
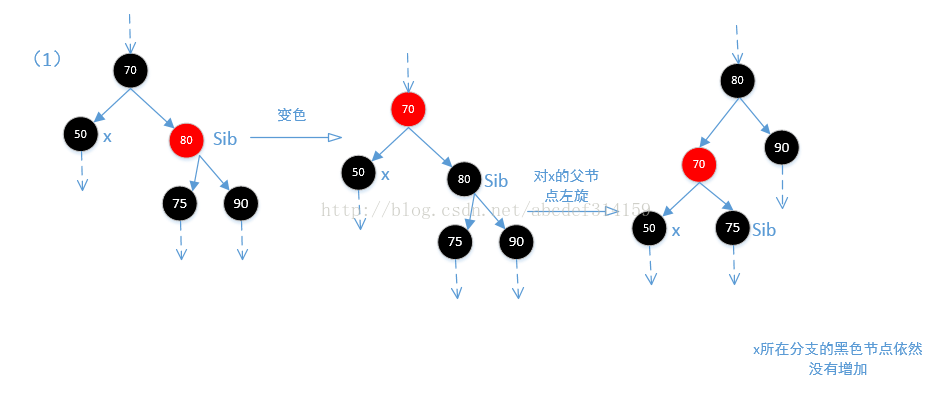
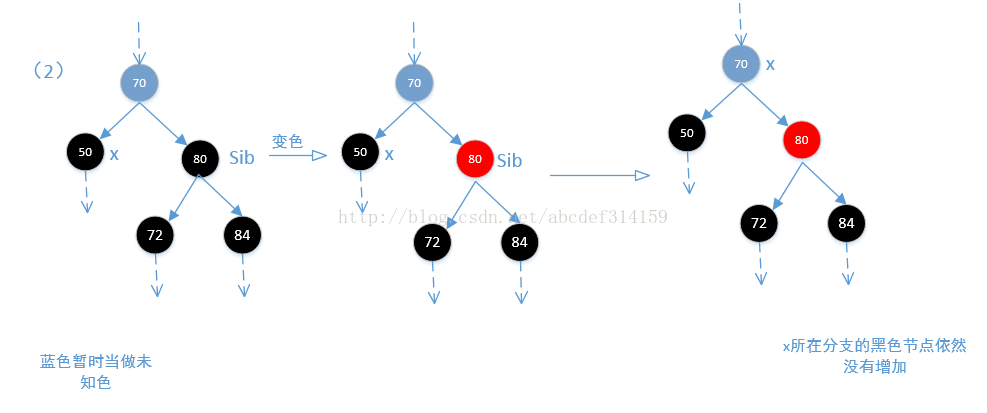
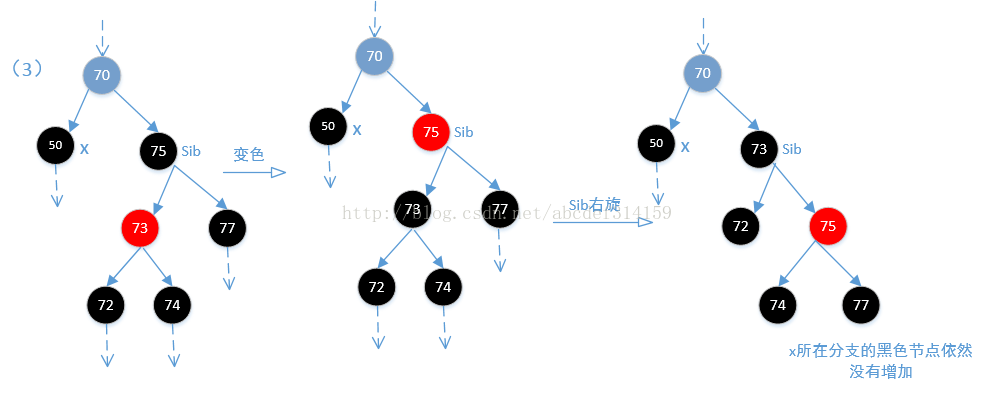
OK，到现在为止put和move方法都已经分析完了，下面看一下其他方法，
getFirstEntry
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
* Returns the first Entry in the TreeMap (according to the TreeMap's
* key-sort function). Returns null if the TreeMap is empty.
*/
//返回第一个节点，最左边的，也是最小值
final TreeMapEntry<K,V> getFirstEntry() {
TreeMapEntry<K,V> p = root;
if (p != null)
while (p.left != null)
p = p.left;
return p;
}
/**
* Returns the last Entry in the TreeMap (according to the TreeMap's
* key-sort function). Returns null if the TreeMap is empty.
*/
//返回最后一个节点，最右边的，也是最大值
final TreeMapEntry<K,V> getLastEntry() {
TreeMapEntry<K,V> p = root;
if (p != null)
while (p.right != null)
p = p.right;
return p;
}
再来看一下containsValue方法
containsValue
1
2
3
4
5
6
7
8
//通过不停的循环查找，先从第一个查找，getFirstEntry()返回的是树的最小值，如果不等，再找比e大的最小值
//successor(e)返回的是e的后继节点，其实就是比e大的最小值，他还可以用于输出排序的大小
public boolean containsValue(Object value) {
for (TreeMapEntry<K,V> e = getFirstEntry(); e != null; e = successor(e))
if (valEquals(value, e.value))
return true;
return false;
}
再来看一个getCeilingEntry，这个方法比较绕
getCeilingEntry
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
* Gets the entry corresponding to the specified key; if no such entry
* exists, returns the entry for the least key greater than the specified
* key; if no such entry exists (i.e., the greatest key in the Tree is less
* than the specified key), returns {@code null}.
*/
//返回最小key大于或等于指定key的节点。
final TreeMapEntry<K,V> getCeilingEntry(K key) {
TreeMapEntry<K,V> p = root;
while (p != null) {
int cmp = compare(key, p.key);
//指定key的节点小于查找的p节点，如果p的左节点（左节点比p小）存在就继续循环，如果不存在就返回p
if (cmp < 0) {
if (p.left != null)
p = p.left;
else
return p;//p节点比key的节点大
} else if (cmp > 0) {//指定的节点大于p节点
if (p.right != null) {//说明key节点比p节点大，如果p的右节点存在，就继续循环，查找更大的
p = p.right;
} else {
//p没有右节点，因为p的左节点是小于p的，既然查找的比p大，所以就往上找p的父节点，因为父节点也比右子节点小，所以要查找到
//父节点是父父节点的左节点为止，这个和查找后继节点其实类似，下面停止循环的条件要么是parent为null，要么ch是父节点的左节点，
//这个可能比较绕，我们先记下面循环停止的父节点是father节点（下面停止的条件是下一个循环的节点是father节点的左节点），在上
//面的循环中，能走到father的左节点这条路线，说明key的节点是小于father节点的，而沿着father节点的左分支一直找下去也没找到大
//于key的节点，这说明father的左节点都是小于key的，所以最后只能网上查找，找到father节点返回。
TreeMapEntry<K,V> parent = p.parent;
TreeMapEntry<K,V> ch = p;
while (parent != null && ch == parent.right) {//如果不为null，是左节点的时候停止循环
ch = parent;
parent = parent.parent;
}
return parent;
}
} else
return p;//如果存在直接返回
}
return null;
}
下面再来看一个和getCeilingEntry方法类似的方法getFloorEntry。
getFloorEntry
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
* Gets the entry corresponding to the specified key; if no such entry
* exists, returns the entry for the greatest key less than the specified
* key; if no such entry exists, returns {@code null}.
*/
//返回最大key小于或等于指定key的节点。
final TreeMapEntry<K,V> getFloorEntry(K key) {
TreeMapEntry<K,V> p = root;
while (p != null) {
int cmp = compare(key, p.key);
if (cmp > 0) {//指定的key大于查找的p，就是查找的p小了
if (p.right != null)//如果存在就循环，查找最大的
p = p.right;
else
return p;//否则就返回p，这个p是小于key的
} else if (cmp < 0) {//说明查找的p大于指定的key，就是查找的p大了
if (p.left != null) {//既然大了，那就往小的找
p = p.left;
} else {
TreeMapEntry<K,V> parent = p.parent;
TreeMapEntry<K,V> ch = p;
//往上找，停止的条件是parent为null，或者ch是父节点的右节点，其实这个方法和getCeilingEntry方法
//非常相似，能走到这一步说明他的父节点比key的大，所以才往左走，当他没有左节点的时候，说明没有
//找到比他小的，但是父节点是比他大的不合适，所以一直往上查找，当查到父节点是父父节点的右节点的
//时候返回，我们暂时记这个父父节点为father，当沿着father的右节点查找的时候，说明key是比father的
//右节点大的，当沿着father的左节点查找的时候说明是要查找比key的小的，但直到最后也没找到的时候，说明
//father的右分支都是都是比key的大，注意只好往上查找，找到father节点，因为father节点是比key的小。
while (parent != null && ch == parent.left) {
ch = parent;
parent = parent.parent;
}
return parent;
}
} else
return p;//正好找到，直接返回
}
return null;
}
getHigherEntry函数和getCeilingEntry函数有点类似，不同点是如果有相同的key，getCeilingEntry会直接返回，而getHigherEntry仍然会返回比key大的最小节点， 同理getLowerEntry函数和getFloorEntry函数很相似，这里就不在详述。下面在看一个方法predecessor
predecessor
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
* Returns the predecessor of the specified Entry, or null if no such.
*/
static <K,V> TreeMapEntry<K,V> predecessor(TreeMapEntry<K,V> t) {
//这个和successor相反，他返回的是前继节点。后继节点返回的是大于t的最小节点，而前继节点返回的是小于
// t的最大节点
if (t == null)
return null;
else if (t.left != null) {//查找t的左节点是最右节点，其实也就是返回小于t的最大值
TreeMapEntry<K,V> p = t.left;
while (p.right != null)
p = p.right;
return p;
} else {
//如果t没有左左子节点，则只能往上找了，因为右节点是大于的，所以不合适，那么往上找也是大于的，那么就只有一个
//找到父节点是父父节点是右节点，返回这个父父节点就行了，这个如果不好理解可以看一下getFloorEntry函数的注释。
//因为一个节点的右节点及右节点的子节点都是大于当前节点的，所以当往左没有找到的时候就往上找，直到找到一个节点是
//父节点的右节点的时候，这个父节点就是小于t的最大节点，这时返回父节点。
TreeMapEntry<K,V> p = t.parent;
TreeMapEntry<K,V> ch = t;
while (p != null && ch == p.left) {
ch = p;
p = p.parent;
}
return p;
}
}
OK，目前为止TreeMap主要方法都已整理完毕。
